chứng minh rằng biểu thức sau đây không phụ thuộc vào giá trị của x
(x+2)^3-x^2(x+6)-4(3x+5)-9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TC
Trên con đường thành công không có....
7 tháng 8 2021
Đúng(2)
Những câu hỏi liên quan
CM
15 tháng 7 2018
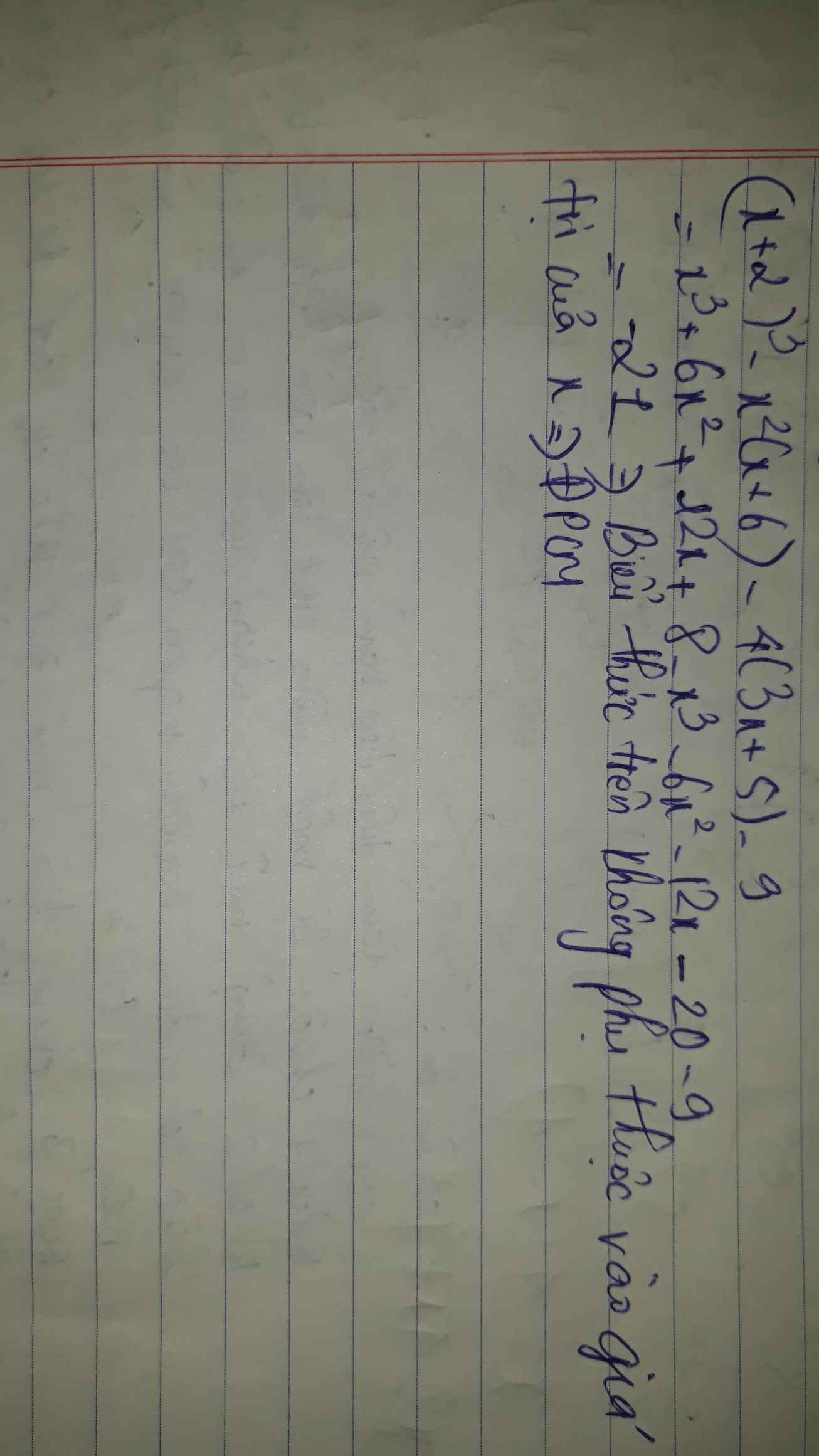
Với x > 0; x ≠ 4; x ≠ 9 ta có:
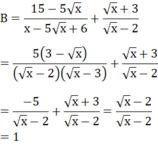
Vậy giá trị của B không phụ thuộc vào giá trị của biến x
28 tháng 10 2021
\(5x^2-\left(2x+1\right)\left(x-2\right)-x\left(3x+3\right)+7\)
\(=5x^2-2x^2+4x-x+2-3x^2-3x+7\)
=9
24 tháng 10 2021
b: \(B=2x\left(x-3\right)-\left(2x-2\right)\left(x-2\right)\)
\(=2x^2-6x-2x^2+4x+2x-4\)
=-4
13 tháng 12 2017
a.=3x2+12x-7x+20+2x3-3x2-2x3-5x
=(3x2-3x2)+(12x-7x-5x)+(2x3-2x3)+20
=20
b.=6x-3-5x+15+18x-24-19x
=(6x-5x+18x-19x)+(-3+15-24)
=-12
2 tháng 7 2019
a) x(3x + 12) - (7x - 20) + x2(2x - 3) - x(2x2 + 5)
<=> x.3x + x.12 - 7x - 20 + x2.2x + x2.(-3) + (-x).2x2 + (-x).5
<=> 3x2 + 12x - 7x - 20 + 2x3 - 3x2 - 2x3 - 5x
<=> (3x2 - 3x2) + (12x - 7x - 5x) - 20 + (2x3 - 2x3)
<=> 0 + 0 - 20 + 0
<=> -20
=> biểu thức không phụ thuộc vào giá trị của biến
b) 3(2x - 1) - 5(x - 3) + 6(3x - 4) - 19x
<=> 3.2x + 3.(-1) + (-5).x + (-5).(-3) + 6.(3x) + 6.(-4) - 19x
<=> 6x - 1 - 5x + 15 + 18x - 24 - 19x
<=> (6x - 5x + 18x - 19x) + (-1 + 15 - 24)
<=> 0 - 10
<=> -10
=> biểu thức không phụ thuộc vào giá trị của biến