Tim giá trị nhỏ nhất của biểu thức E = 5x2 +8xy + 5y2 – 2x + 2y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NP
1
Những câu hỏi liên quan
GS
23 tháng 7 2021
\(5x2+5y2+8xy-2x+2y+2=0\)
(=) \((4x^2 + 8xy + 4y^2) + (x^2 - 2x +1) + (y^2 + 2y +1) = 0 \)
(=) \(4(x+y)^2 + (x-1)^2 + (y+1)^2 = 0 \)
Ta có \(\begin{cases} 4(x+y)^2 ≥ 0 \\ (x-1)^2 ≥ 0 \\ (y+1)^2 ≥ 0 \end{cases} \)
=> \(4(x+y)^2 + (x-1)^2 + (y+1)^2 ≥ 0 \)
Vậy để \(4(x+y)^2 + (x-1)^2 + (y+1)^2 = 0 \)
(=) \(\begin{cases} 4(x+y)^2 = 0 \\ (x-1)^2 = 0 \\ (y+1)^2 = 0 \end{cases} \)
(=) \(\begin{cases} x = -y \\ x = 1 \\ y = -1 \end{cases} \)
(=) \(\begin{cases} x = 1 \\ y = -1 \end{cases} \)
Vậy \(M=(x+y)^{2015}+(x-2)^{2016}+(y+1)^{2017} M=(1-1)^{2015} + (1-2)^{2016} + (-1+1)^{2017} M=0^{2015} + (-1)^{2016} +0^{2017} M= 1 \)Vậy M = 1
1 tháng 11 2023
Sửa đề: \(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(\left(2x+2y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(\left\{{}\begin{matrix}2x+2y=0\\x-1=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(M=\left(x-y\right)^{2023}-\left(x-2\right)^{2024}+\left(y+1\right)^{2023}\)
\(=\left(1+1\right)^{2023}-\left(1-2\right)^{2024}+\left(-1+1\right)^{2023}\)
\(=2^{2023}-1\)
G
1
12 tháng 9 2017
\(E=5x^2+8xy+5y^2-2x+2y\)
\(=\left(4x^2+8xy+4y^2\right)+\left(x^2-2x+1\right)+\left(y^2+2y+1\right)-2\)
\(=4\left(x^2+2xy+y^2\right)+\left(x^2-2x+1\right)+\left(y^2+2y+1\right)-2\)
\(=4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2-2\ge-2\) có GTNN là - 2
Dấu "=" xảy ra \(\Leftrightarrow x=1;y=-1\)
Vậy \(E_{min}=-2\) tại \(x=1;y=-1\)
MA
2
7 tháng 11 2021
ko có 2x2 đâu mik thấy đề bài nó ghi như thế. bn giúp mik nhé!
K
2
22 tháng 7 2021
A = x^2 + 5y^2 + 4xy - 2y - 3
= x^2 + 4xy + 4y^2 + y^2 - 2y + 1 - 4
= ( x + 2y )^2 + ( y - 1 )^2 - 4 >= -4
Dấu ''='' xảy ra khi y = 1 ; x = -2
Vậy GTNN A là -4 khi x = -2 ; y = 1
PV
1
16 tháng 11 2021
=4x2+4xy+y2+x2-6x-2y+1
=(2x+y)2-4x-2y+1+x2-2x+1-1
=[(2x+y)2-2(2x+y)+1]+(x-1)2-1
=(2x+y+1)2+(x-1)2-1
ta có: (2x+y+1)2\(\ge0\)với\(\forall\)x
(x-1)2\(\ge0\)với \(\forall\)x
\(\Rightarrow\left(2x+y+1\right)^2+\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(2x+y+1\right)^2+\left(x+1\right)^2-1\ge-1\forall x\)
\(\Rightarrow N\ge-1\)
Dấu '=' xảy ra\(\Leftrightarrow\hept{\begin{cases}\left(2x+y+1\right)^2=0\\\left(x-1\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=-3\end{cases}}}\)
vậy N đạt GTNN là -1 khi và chỉ khi x=1;y=-3
5 tháng 9 2021
\(a,9x^2+y^2+2z^2-18x+4z-6y+20=0\\ \Leftrightarrow9\left(x-1\right)^2+\left(y-3\right)^2+2\left(z+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\\z=-1\end{matrix}\right.\)
\(b,5x^2+5y^2+8xy+2y-2x+2=0\\ \Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-y\\x=1\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(c,5x^2+2y^2+4xy-2x+4y+5=0\\ \Leftrightarrow\left(2x+y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x=-y\\x=1\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(d,x^2+4y^2+z^2=2x+12y-4z-14\\ \Leftrightarrow\left(x-1\right)^2+\left(2y-3\right)^2+\left(z+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{3}{2}\\z=-2\end{matrix}\right.\)
\(e,x^2+y^2-6x+4y+2=0\\ \Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
Pt vô nghiệm do ko có 2 bình phương số nguyên có tổng là 11
5 tháng 9 2021
e: Ta có: \(x^2-6x+y^2+4y+2=0\)
\(\Leftrightarrow x^2-6x+9+y^2+4y+4-11=0\)
\(\Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
Dấu '=' xảy ra khi x=3 và y=-2
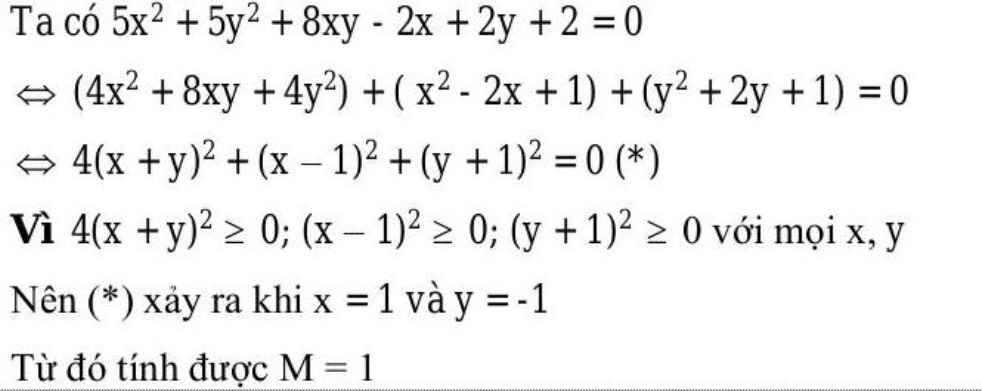
dg bận nên mk ghi kq thôi từ kq bn suy ra hạng tử r` pt nhé
Min=-2 khi (x,y)=(1,-1)