Cho tam giác ABC vuông vân tại A có I thuộc BC.Vẽ BE và CF vuông góc với AI
CM: AB2=BE2+CF2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 9 2019
Xét \(\Delta\) vuông BEM và \(\Delta\)vuông CFM ta có :
BM = CM
EMB = CMF ( đối đỉnh )
=> \(\Delta\)BEM = \(\Delta\)CFM ( cạnh huyền - góc nhọn )
=> BE = CF
7 tháng 4 2023
a: Xét tứ giác AQHP có
AQ//HP
AP//HQ
=>AQHP là hình bình hành
Xet ΔAHQ và ΔHAP có
HA chung
HQ=AP
AQ=HP
=>ΔAHQ=ΔHAP
b: ΔFBC vuông tại F
mà FM là trung tuyến
nên FM=BC/2
ΔECB vuông tại E
mà EM là trung tuyến
nên EM=BC/2=FM
=>ΔMEF cân tại M
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AEF=góc ABC
6 tháng 8 2021
a) Ta có:
IE\(\perp\)AC (I\(\in\)BE mà BE \(\perp\)AC)
MQ\(\perp\)AC (GT)
\(\Rightarrow\)IE // MQ
Lại có:
MI \(\perp\)BE (GT)
EQ\(\perp\) BE (E;Q\(\in\)AC ; BE\(\perp\)AC)
\(\Rightarrow\)MI // EQ
mà IE // MQ (CMT)
Vậy tứ giác MIEQ có các cạnh đối song song.
b) Vì: MI // EQ (CMT)
\(\Rightarrow\)\(\widehat{ACB}\)=\(\widehat{IMB}\) (Đồng vị)
mà \(\widehat{ABC}=\widehat{ACB}\) (TG ABC cân tại A)
\(\Rightarrow\)\(\widehat{ABC}=\widehat{IMB}\)
Xét tg BKM vg tại K và tg MIB vg tại I
BM chung
\(\widehat{ABC}=\widehat{IMB}\)(CMT)
Vậy: TG BKM=TG MIB (CH-GN)
c) Vì: TG BKM=TG MIB (CMT)
\(\Rightarrow\)MK=BI ( CTỨ)
Xét tg IEM vg tại I và tg QME vg tại Q:
EM chung
\(\widehat{IEM}=\widehat{EMQ}\)(Soletrong do IE // MQ)
Vậy TG IEM= TG QME (CH-GN)
\(\Rightarrow\)MQ=IE (CTỨ)
Ta có: BE= BI + IE (B,I,E thẳng hàng)
mà\(\hept{\begin{cases}BI=MI\left(CMT\right)\\IE=MQ\left(CMT\right)\end{cases}}\)
\(\Rightarrow\)BE=MK+MQ
7 tháng 8 2023
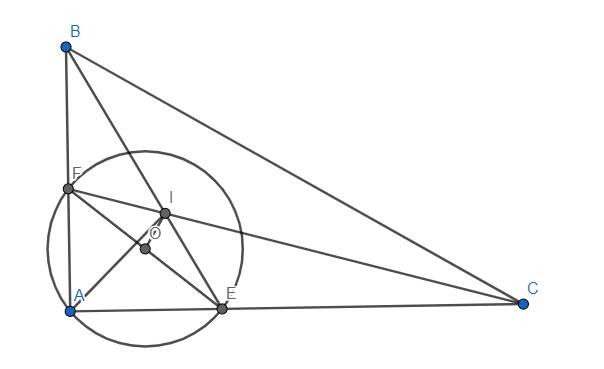
Theo tính chất quen thuộc, O là tâm của (AEF).
Mặt khác, ta lại có \(\widehat{BIC}=90^o+\dfrac{\widehat{BAC}}{2}=135^o\) nên \(\widehat{BIF}=45^o\). Lại có \(\widehat{BAI}=45^o\) nên \(\Delta BIF~\Delta BAI\left(g.g\right)\) \(\Rightarrow\dfrac{BI}{BA}=\dfrac{BF}{BI}\Rightarrow BI^2=BA.BF\) \(\Rightarrow P_{B/\left(O\right)}=P_{B/\left(I;0\right)}\)
\(\Rightarrow\) B nằm trên trục đẳng phương của (O) và (I;0).
Hoàn toàn tương tự, ta chứng minh được C nằm trên trục đẳng phương của (O) và (I;0). Từ đó suy ra BC là trục đẳng phương của (O) và (I;0) \(\Rightarrow BC\perp OI\) (đpcm)
25 tháng 8 2023
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE/AB=AF/AC
Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc FAE chung
Do đó: ΔAEF đồng dạng với ΔABC
=>góc AEF=góc ABC
b: Kẻ HM//AB(M thuộc AC)
HN//AC(N thuộc AB)
Xét tứ giác AMHN có
AM//HN
AN//HM
Do đó: AMHN là hình bình hành
=>AM=HN; AN=HM
ΔAHM có AH<AM+MH
=>AH<AM+AN
HN//AC
mà BH vuông góc AC
nên HB vuông góc HN
ΔHBN vuông tại H
=>HB<BN
HM//AB
CH vuông góc AB
Do đó: HC vuông góc HM
=>ΔHCM vuông tại H
=>HC<MC
AH<AM+AN
HB<BN
HC<MC
=>HA+HB+HC<AM+AN+BN+MC=AC+AB
Chứng minh tương tự, ta được:
HA+HB+HC<AB+BC và HA+HB+HC<AC+BC
=>3*(HA+HB+HC)<2(BA+BC+AC)
=>HA+HB+HC<2/3*(BA+BC+AC)
30 tháng 4 2022
a: Xet ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
b: Xét ΔAFM vuông tại F và ΔAEM vuông tại E có
AM chung
AF=AE
Do đó: ΔAFM=ΔAEM
Suy ra: \(\widehat{BAM}=\widehat{CAM}\)
hay AM là tia phân giác của góc BAC