Giúp mình câu 2, 3 nhá, huhu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




96-3(x+1)=42
3(x+1) = 96-42
3(x+1) = 54
x+1 = 54:3
x = 18-1
x = 17
Mình chỉ giúp đc bài này thôi nhé

a.
\(\Leftrightarrow\left(sinx+cosx\right)\left(1+sinx.cosx\right)=1\)
Đặt \(sinx+cosx=t\) \(\Rightarrow-\sqrt{2}\le t\le\sqrt{2}\)
\(t^2=1+2sinx.cosx\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình trở thành:
\(t\left(1+\dfrac{t^2-1}{2}\right)=1\)
\(\Leftrightarrow t^3+t-2=0\)
\(\Leftrightarrow\left(t-1\right)\left(t^2+t+2\right)=0\)
\(\Leftrightarrow t=1\)
\(\Rightarrow sinx+cosx=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}=sin\left(\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow...\)
b.
Đặt \(sinx-cosx=t\Rightarrow-\sqrt{2}\le t\le\sqrt{2}\)
\(t^2=1-2sinx.cosx\Rightarrow sinx.cosx=\dfrac{1-t^2}{2}\)
Phương trình trở thành:
\(t^3=1+\dfrac{1-t^2}{2}\)
\(\Leftrightarrow2t^3+t^2-3=0\)
\(\Leftrightarrow\left(t-1\right)\left(2t^2+3t+3\right)=0\)
\(\Leftrightarrow t=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}=sin\left(\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow...\)

b.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cos2x-\dfrac{1}{2}sin2x=-cosx\)
\(\Leftrightarrow cos\left(2x+\dfrac{\pi}{6}\right)=cos\left(x+\pi\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{6}=x+\pi+k2\pi\\2x+\dfrac{\pi}{6}=-x-\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{6}+k2\pi\\x=-\dfrac{7\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
c.
\(\Leftrightarrow2cos4x.sin3x=2sin4x.cos4x\)
\(\Leftrightarrow cos4x\left(sin4x-sin3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\sin4x=sin3x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{\pi}{2}+k\pi\\4x=3x+k2\pi\\4x=\pi-3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=k2\pi\\x=\dfrac{\pi}{7}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
2.
\(f\left(x\right)=\dfrac{1}{2}-\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x-5\)
\(=-\dfrac{9}{2}-\left(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x\right)\)
\(=-\dfrac{9}{2}-cos\left(2x-\dfrac{\pi}{3}\right)\)
Do \(-1\le-cos\left(2x-\dfrac{\pi}{3}\right)\le1\Rightarrow-\dfrac{11}{2}\le y\le-\dfrac{7}{2}\)
\(y_{min}=-\dfrac{11}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
\(y_{max}=-\dfrac{7}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\Rightarrow x=\dfrac{2\pi}{3}+k\pi\)

Bài làm
2X x 2 + ( -3 ) x 3 : 9 = 0
4x - 1 = 0
4x = 1
x = \(\frac{1}{4}\)
Vậy x =\(\frac{1}{4}\)
# Học tốt #

\(\Delta'=3-\left(-6\right)=9>0\)
vậy pt có 2 nghiệm pb
\(x_1=\sqrt{3}-3;x_2=\sqrt{3}+3\)






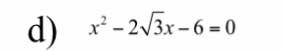
2)
1 phân tử MgCO3 có khối lượng 84 đvC
Suy ra : số phân tử MgCO3 là 840 : 84 = 10 phân tử
Suy ra : có 10 nguyên tử Magie, 10 nguyên tử Cacbon và 30 nguyên tử Oxi
3)
Ta có : $56.2 + 96n = 400 \Rightarrow n = 3$
mà $SO_4$ có hóa trị II
Theo quy tắc hóa trị, ta tìm được Fe có hóa trị III trong hợp chất
2)
1 phân tử MgCO3 có khối lượng 84 đvC
Suy ra : số phân tử MgCO3 là 840 : 84 = 10 phân tử
Suy ra : có 10 nguyên tử Magie, 10 nguyên tử Cacbon và 30 nguyên tử Oxi
3)
Ta có : 56.2+96n=400⇒n=356.2+96n=400⇒n=3
mà SO4SO4 có hóa trị II
Theo quy tắc hóa trị, ta tìm được Fe có hóa trị III trong hợp chất