Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Biên độ dao động \(A = - 5\); Pha ban đầu của dao động: \(\varphi = 0\)
b) Pha dao động tại thời điểm \(t = 2\) à \(\omega t + \varphi = 4\pi .2 = 8\pi \)
Chu kỳ \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = 0,2\)
Trong khoảng thời gian 2 giây, số dao động toàn phần vật thực hiện được là: \(\frac{2}{{0,2}} = 10\) (dao động)
Ta có: \(x\left( t \right) = {x_1}\left( t \right) + {x_2}\left( t \right) = 2\left[ {\cos \left( {\frac{\pi }{3}t + \frac{\pi }{6}} \right) + \cos \left( {\frac{\pi }{3}t - \frac{\pi }{3}} \right)} \right]\)
\(2\left[ {\cos \left( {\frac{{\frac{\pi }{3}t + \frac{\pi }{6} + \frac{\pi }{3}t - \frac{\pi }{3}}}{2}} \right).\cos \left( {\frac{{\frac{\pi }{3}t + \frac{\pi }{6} - \frac{\pi }{3}t + \frac{\pi }{3}}}{2}} \right)} \right] = 2\left[2. {\cos \left( {\frac{\pi }{3}t - \frac{\pi }{{12}}} \right).\cos \frac{\pi }{4}} \right] = 2\sqrt 2 \cos \left( {\frac{\pi }{3}t - \frac{\pi }{{12}}} \right)\)
Vậy biên độ là \(2\sqrt 2 \), pha ban đầu \( - \frac{\pi }{{12}}\)
Đáp án C
Phương pháp: Sử dụng lí thuyết về tổng hợp hai hai động điều hòa cùng tần số và năng lượng dao động điều hòa
Cách giải:
+ Do hai dao động vuông pha nên biên độ dao động tổng hợp là: A = A 1 2 + A 2 2
+ Cơ năng dao động của vật:
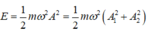
=> Khối lượng vật m = 2 E ω 2 ( A 1 2 + A 2 2 ) => Chọn C
Cơ năng:
\(W=\dfrac{1}{2}m.v_{max}^2=0,5.m.(\omega.A)^2=0,5.m\omega^2A^2\)
Chọn A.