Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vật đi qua vị trí cân bằng theo chiều dương :
\(\left\{{}\begin{matrix}x_0=0\\v_0>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A\cdot cos\varphi=0\\-\omega A\cdot sin\varphi>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=0\\sin\varphi< 0\end{matrix}\right.\)
\(\Leftrightarrow\varphi=\dfrac{-\pi}{2}\)
\(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
=> B

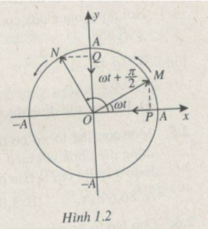
Vì cos ω t = sin( ω t + π /2) nên dao động của điểm Q trên trục y có thể viết dưới dạng y = Acos ω t. Vì vậy hiệu số pha giữa hai dao động của P và Q bằng 0.

Đáp án A
Vật đi được quãng đường 2A trong khoảng thời gian
![]()
![]()
Tại t=0 vật đang chuyển động qua vị trí x=0,5A theo chiều âm, đến thời điểm t=2/3 (s) ứng với một phần 3 chu kỳ vật đến vị trí biên âm
![]()

Đáp án C
Trong phương trình dao động x = Acos(ωt + φ) thì ω gọi là tần số góc của dao động

Đáp án C
Phương pháp: Sử dụng lí thuyết về tổng hợp hai hai động điều hòa cùng tần số và năng lượng dao động điều hòa
Cách giải:
+ Do hai dao động vuông pha nên biên độ dao động tổng hợp là: A = A 1 2 + A 2 2
+ Cơ năng dao động của vật:
=> Khối lượng vật m = 2 E ω 2 ( A 1 2 + A 2 2 ) => Chọn C