Một vật giao động điều hòa với phương trình \(x=A\cos\left(\omega t+\frac{\pi}{3}\right)\), chu kì T. Kể từ thời điểm từ ban đầu thì thời gian bằng bao nhiêu lần chu kì, vật qua vị trí cân bằng theo chiều âm lần thứ 2011?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Ban đầu vật ở vị trí biên → vật đến vị trí cân bằng lần đầu sau khoảng thời gian T 4 . Vật sẽ mất thêm đúng 1 chu kì nữa để đi qua vị trí này hai lần tiếp theo, vậy tổng thời gian là △ t = 5 T 4

Đáp án C
+ Ban đầu vật ở vị trí biên → vật đến vị trí cân bằng lần đầu sau khoảng thời gian T 4 . Vật sẽ mất thêm đúng 1 chu kì nữa để đi qua vị trí này hai lần tiếp theo, vậy tổng thời gian là ∆ t = 5 T 4

Đáp án B
+ Vận tốc của vật bằng 0 tại biên -> khoảng thời gian vật đi từ vị trí cân bằng đến biên là 0,25T

Đáp án B
Trong dao động điều hòa vận tốc của vật bằng 0 khi vật ở vị trí biên.
Mà có t = 0 tại VTCB → trong nửa chu kì đầu tiên vận tốc bằng 0 ở thời điểm t = T/4

Đáp án B
Vận tốc của vật bằng 0 tại vị trí biên, thời gian để vật đi từ vị trí cân bằng đến vị trí biên là 0,25T

Chọn B
+ Vận tốc của vật bằng không khi vật ở vị trí biên. Vật xuất phát từ vị trí cân bằng nên trong nửa chu kì đầu tiên vật sẽ đi tới biên âm rồi quay trở về đúng vị trí cân bằng nên vận tốc của vật bằng không ở thời điểm T/4.


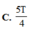
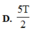

Lúc t=0 vật ở vị trí có li độ là A/2.
Do có yêu cầu chiều âm nên t2011=t1 + (2011-1)T
Từ A/2 theo chiều âm đến cân bằng là T/12 suy ra t2011= T/12+2010T=\(\frac{24121T}{12}\)
+ Biểu diễn dao động này bằng véc tơ quay.
+ Sau mỗi chu kì, chất điểm qua VTCB theo chiều âm 1 lần.
Như vậy, sau 2010 chu kì, chất điểm qua VTCB theo chiều âm là 2010 lần.
+ Lần cuối cùng véc tơ quay 1 góc 300 để đến VTCB theo chiều âm.
Như vậy, thời gian ở lần cuối là \(\dfrac{30}{360}T=T/6\)
Vậy, tổng thời gian là: \((2010+1/6).T\)