Cho \(\Delta ABC\) cân tại A, đường cao AH = 4cm, biết BC = 6cm.
Cắt \(\Delta ABC\) thành ba mảnh để ghép lại thành một hình chữ nhật. Tính diện tích mồi mảnh.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AB=căn 5^2-4^2=3cm
Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*BC; AH*BC=AB*AC
=>AH=3*4/5=2,4cm; BH=3^2/5=1,8cm
CH=5-1,8=3,2cm
b: C=3+4+5=12cm
S=1/2*3*4=6cm2
AM=BC/2=2,5cm
c: MA=MC=2,5cm
AC=4cm
ΔMAC cân tại M có MI là đường cao
nên I là trung điểm của AC
=>IA=IC=AC/2=2cm
MI=căn MA^2-IA^2=1,5cm

a, bạn tự làm nhé
b, Xét tam giác ABH và tam giác CAH ta có
^AHB = ^CHA = 900
^ABH = ^CAH ( cùng phụ ^BAH )
Vậy tam giác ABH ~ tam giác CAH ( g.g )
\(\Rightarrow\frac{AH}{CH}=\frac{BH}{AH}\Rightarrow AH^2=BH.CH\)
c, mình làm hơi tắt nhé, bạn dùng tỉ lệ thức xác định tam giác đồng dạng nhé
Dễ có : \(AH^2=AK.AC\)(1)
\(AH^2=AI.AB\)(2)
Từ (1) ; (2) suy ra : \(AK.AC=AI.AB\Rightarrow\frac{AK}{AB}=\frac{AI}{AC}\)
Xét tam giác AIK và tam giác ACB
^A _ chung
\(\frac{AK}{AB}=\frac{AI}{AC}\)( cmt )
Vậy tam giác AIK ~ tam giác ACB ( c.g.c )

Xét △ ABC. Kẻ đường cao AH. Gọi M là trung điểm của AC, N là trung điểm của AB.
Từ M kẻ đường thẳng song song AH cắt BC tại K
Từ N kẻ đường thẳng song song AH cắt BC tại L
Từ A kẻ đường thẳng song song BC cắt hai đường thẳng MK và NL tại T và R
Ta có: △ MKC = △ MTA
△ NLB = △ NAR
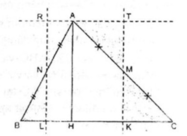
Cắt △ ABC theo đường MK và NL ta ghép lại được một hình chữ nhật KTRL có diện tích bằng diện tích tam giác ABC

Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân

a) Xét \(\Delta ABC\)và \(\Delta HBA\)có:
\(\widehat{B}\) chung
\(\widehat{BAC}=\widehat{BHA}=90^0\)
suy ra: \(\Delta ABC~\Delta HBA\) (g.g)
b) Xét \(\Delta AIH\)và \(\Delta AHB\)có:
\(\widehat{AIH}=\widehat{AHB}=90^0\)
\(\widehat{IAH}\) chung
suy ra: \(\Delta AIH~\Delta AHB\) (g.g)
\(\Rightarrow\)\(\frac{AI}{AH}=\frac{AH}{AB}\) \(\Rightarrow\) \(AI.AB=AH^2\) (1)
Xét \(\Delta AHK\)và \(\Delta ACH\)có:
\(\widehat{HAK}\)chung
\(\widehat{AKH}=\widehat{AHC}=90^0\)
suy ra: \(\Delta AHK~\Delta ACH\) (g.g)
\(\Rightarrow\)\(\frac{AH}{AC}=\frac{AK}{AH}\)
\(\Rightarrow\)\(AK.AC=AH^2\) (2)
Từ (1) và (2) suy ra: \(AI.AB=AK.AC\)
c) \(S_{ABC}=\frac{1}{2}.AH.BC=20\)cm2
Tứ giác \(HIAK\)có: \(\widehat{HIA}=\widehat{IAK}=\widehat{AKH}=90^0\)
\(\Rightarrow\)\(HIAK\)là hình chữ nhật
\(\Rightarrow\)\(AH=IK=4\)cm
Ta có: \(AI.AB=AK.AC\) (câu b)
\(\Rightarrow\)\(\frac{AI}{AC}=\frac{AK}{AB}\)
Xét \(\Delta AIK\)và \(\Delta ACB\)có:
\(\widehat{IAK}\)chung
\(\frac{AI}{AC}=\frac{AK}{AB}\) (cmt)
suy ra: \(\Delta AIK~\Delta ACB\) (c.g.c)
\(\Rightarrow\)\(\frac{S_{AIK}}{S_{ACB}}=\left(\frac{IK}{BC}\right)^2=\frac{4}{25}\)
\(\Rightarrow\)\(S_{AIK}=\frac{4}{25}.S_{ACB}=3,2\)cm2

2:
a: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạng với ΔHCA
=>HA/HC=HB/HA
=>HA^2=HB*HC
b: BC=4+9=13cm
AH=căn 4*9=6cm
S ABC=1/2*6*13=39cm2

Câu 1 :
Nửa chu vi hình chữ nhật là :
92 : 2 = 46 ( m )
Nếu tăng chiều rộng 5 m và giảm chiều dài 5 m thì mảnh vườn trở thành hình vuông . Vậy lúc đầu chiều dài hơn chiều rộng : 5 x 2 = 10 ( m )
Chiều dài mảnh vườn hình chữ nhật là ;
( 46 + 10 ) : 2 = 28 ( m )
Chiều rộng mảnh vườn hình chữ nhật là :
46 - 28 = 18 ( m )
Diện tích mảnh vườn là :
18 x 28 = 504 ( m2)
Đáp số : 504 m2
Câu 2 :
a) Chiều cao hình tam giác ABC là :
30 x 2/3 = 20 ( cm )
Diện tích tam giác ABC là :
30 x 20 : 2 = 300 ( cm2)
b) Diện tích tam giác ACM là :
300 x 20 : 100 = 60 ( cm2)
Vì tam giác ACM có cùng chiều cao AH với tam giác ABC nên độ dài cạnh CM là :
60 x 2 : 20 = 6 ( cm )
Đáp số : a) 300 cm2
b) 6 cm