trong mặt phẳng oxy cho tam giác ABC A(2;4) B(-6;0) C(2;0) tìm K sao cho K thuộc Oy và KA + KB +KC nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
21 tháng 1 2021
a, Gọi \(I\left(x;y\right)\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}IA=IB\\IA=IC\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}IA^2=IB^2\\IA^2=IC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-3-x\right)^2+\left(6-y\right)^2=\left(1-x\right)^2+\left(-2-y\right)^2\\\left(-3-x\right)^2+\left(6-y\right)^2=\left(6-x\right)^2+\left(3-y\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=-5\\3x-y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
CM
25 tháng 10 2018
Chọn D
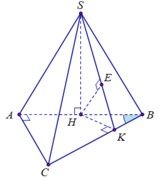
Ta có tam giác ABC vuông tại A góc A B C ^ = 30 o và BC = a, suy ra AC = a 2 , AB = a 3 2
Lại có S A B ⊥ A B C C A ⊥ A B ⇒ A C ⊥ S A B , suy ra tam giác SAC vuông tại A.
Suy ra S A = S C 2 - A C 2 = a 2 - a 2 2 = a 3 2
Tam giác SAB có S A = a 3 2 , A B = a 3 2 , S B = a SB=a. Từ đó sử dụng công thức Hê-rông ta tính được S S A B = a 2 2 4 ⇒ S H = 2 S S A B A B = a 6 3 ⇒ B H = a 3 3 = 2 A B 3 .
Suy ra d(H,(SBC)) = 2 3 d A , S B C . Từ H kẻ H K ⊥ B C .
Kẻ H E ⊥ S K ⇒ H E ⊥ S B C
Ta dễ tính được H K = a 3 6 ⇒ d H , S B C = a 6 9 .
Vậy d A , S B C = 3 2 d H , S B C = 3 2 . a 6 9 = a 6 6 .