cho Δ1 :x+2y+4=0
Δ2 : 2x-y+6=0
a,Tính góc giữa 2 đường thẳng Δ1,Δ2
b,Tính KC từ A (3;1) tới đường thẳng Δ1
c,Xét vị trí tương đối của Δ1 và Δ2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 6 2018
Hai đường thẳng Δ1 và Δ2 có vecto pháp tuyến lần lượt là: n1→(2;1); n2→(5;-2)
Góc giữa hai đường thẳng (Δ1) và (Δ2) là:
CM
18 tháng 2 2017
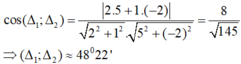
Chọn C.
Ta có:
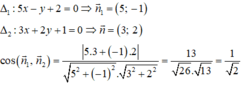
Vậy góc giữa hai đường thẳng Δ1, Δ2 là 45 ° .
CM
29 tháng 6 2019
Cách 1:
Δ1: y = –2x + 4 ⇔ 2x + y – 4 = 0
Δ2: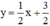 
⇔ x - 2y + 3 = 0
Hai đường thẳng Δ1 và Δ2 có vecto pháp tuyến lần lượt là: n1→(2;1); n2→(1;-2)
Góc giữa (Δ1) và (Δ2):
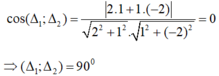
Cách 2:
Δ1: y = –2x + 4 có hệ số góc k1 = –2
Δ2: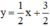 
có hệ số góc k2 = 1/2
Nhận thấy k1.k2 = –1 nên Δ1 ⊥ Δ2 ⇒ (Δ1, Δ2) = 90°.
CM
2 tháng 8 2017
Đáp án D
Mặt cầu (S) có tâm I 1 ; − 2 ; 0 và bán kính R = 21
Đường thẳng Δ 1 có vtcp u 1 → = 2 ; − 3 ; 2 và đường thẳng Δ 2 có vtcp u 2 → = 1 ; 1 ; − 1
Mặt phẳng α có vtcp n → = u 1 → , u 2 → = 1 ; 4 ; 5 ⇒ α : x + 4 y + 5 z + m = 0
Do tiếp xúc với mặt cầu (S) nên
d I , α = 21 ⇔ 1 + 4. − 2 + 5.0 + m 1 2 + 4 2 + 5 2 = 21 ⇔ m = 7 + 21 2 m = 7 − 21 2
Do α cắt trục Oz tại điểm có cao độ dương ta có phương trình của α : x + 4 y + 5 z + 7 − 21 2 = 0
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2023
Thay tọa độ A vào 2 pt đường thẳng không thỏa mãn, vậy đó là 2 pt đường thẳng của các cạnh BC và CD
\(\Rightarrow\) Khoảng cách từ A đến 2 đường thẳng nói trên bằng độ dài 2 cạnh của hcn
\(\Rightarrow S=d\left(A;\Delta_1\right).d\left(A;\Delta_2\right)=\dfrac{\left|3-2.\left(-1\right)+1\right|}{\sqrt{1^2+\left(-2\right)^2}}.\dfrac{\left|2.3-1\right|}{\sqrt{2^2+1^2}}=6\)