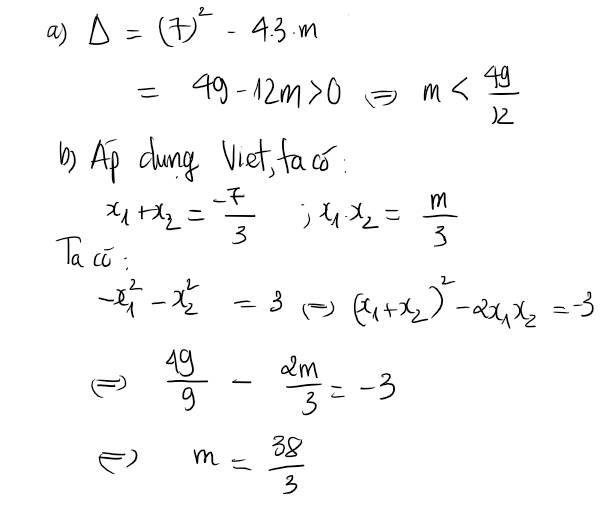Điều kiện của để hệ phương trình có nghiệm mà là m < (Nhập kết quả dưới dạng số thập phân gọn...
Đọc tiếp
Điều kiện của để hệ phương trình
có nghiệm
mà
là m <
(Nhập kết quả dưới dạng số thập phân gọn nhất)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DH
0
Những câu hỏi liên quan
CM
18 tháng 6 2018
Với m = -2 thì (*) trở thành: 0x = 0 ( luôn đúng với mọi x). Khi đó, hệ phương trình có vô số nghiệm
Với m= -4 thì (*) trở thành: 0x = -10 ( vô lí) do đó hệ phương trình đã cho có vô nghiệm
Với m ≠ 2 ; m ≠ 4 thì (*) có nghiệm duy nhất nên hệ phương trình đã cho có nghiệm duy nhất.
Vậy điều kiện cần và đủ để hệ phương trình có nghiệm là m ≠ 2
Chọn A
MN
28 tháng 5 2021
\(mx+2y=-1\)
\(\text{Với : }\)\(\left(x,y\right)=\left(3,2\right)\)
\(3m+2\cdot2=-1\)
\(\Leftrightarrow m=\dfrac{-5}{3}\)
TA
28 tháng 5 2021
`(x;y)=(3;2)` là nghiệm của hệ (I) `<=> m.3+2.2=-1 <=> m=-5/3`
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
4 tháng 6 2023
Em nên chèn bằng công thức nhé, chứ em viết thế này cô không hiểu đúng đề bài em cần được để trợ giúp em đâu
CM
20 tháng 3 2018
Ta có x + 2 y = 2 m x − y = m
⇔ x = 2 − 2 y m 2 − 2 y − y = m ⇔ x = 2 − 2 y 2 m + 1 y = m
Để phương trình có nghiệm duy nhất thì m ≠ - 1 2
Suy ra y = m 2 m + 1 ⇒ x = 2 − 2. m 2 m + 1 ⇒ x = 2 m + 2 2 m + 1
Vậy hệ có nghiệm duy nhất x = 2 m + 2 2 m + 1 y = m 2 m + 1
Để x > 1 y > 0
⇔ 2 m + 2 2 m + 1 > 1 m 2 m + 1 > 0 ⇔ 1 2 m + 1 > 0 m 2 m + 1 > 0 ⇔ 2 m + 1 > 0 m > 0 ⇔ m > − 1 2 m > 0 ⇒ m > 0
Kết hợp điều kiện m ≠ - 1 2 ta có m > 0
Đáp án: A
29 tháng 7 2023
a: Để phương trình có nghiệm thì (-2)^2-4(m-3)>=0
=>4-4m+12>=0
=>-4m+16>=0
=>-4m>=-16
=>m<=4
b: x1-x2=4
x1+x2=2
=>x1=3; x2=-1
x1*x2=m-3
=>m-3=-3
=>m=0(nhận)
17 tháng 2 2021
a) Ta có: \(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(2m-3\right)=16-4\left(2m-3\right)\)
\(\Leftrightarrow\Delta=16-8m+12=-8m+28\)
Để phương trình có hai nghiệm x1;x2 phân biệt thì \(-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Với \(m< \dfrac{7}{2}\) thì phương trình có hai nghiệm phân biệt x1;x2
nên Áp dụng hệ thức Viet, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-4\right)}{1}=4\\x_1\cdot x_2=\dfrac{2m-3}{1}=2m-3\end{matrix}\right.\)
Để phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau thì
\(\left\{{}\begin{matrix}m< \dfrac{7}{2}\\4+2m-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\m=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy: Khi \(m=-\dfrac{1}{2}\) thì phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau
CM
25 tháng 2 2017
- Ta có: x, y là nghiệm phương trình X 2 - S X + P = 0
- Hệ phương trình có nghiệm khi ∆ = S 2 - 4 P ≥ 0
Đáp án cần chọn là: D