K = [ (x+1/x-1) - ( x-1 /x+1 ) +( x^2-4x1 /x^2-1)].x+2003/x a) tìm điều kiện dể K xác định
b)rút gọn K
c)với giá trị nguyên nào của x để K nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
0
3 tháng 3 2022
a: ĐKXĐ: \(x\notin\left\{1;-1;0\right\}\)
b: \(K=\dfrac{x^2+2x+1-x^2+2x-1+x^2-4x-1}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+2003}{x}\)
\(=\dfrac{x^2-1}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+2003}{x}=\dfrac{x+2003}{x}\)
c: Để K là số nguyên thì \(x\inƯ\left(2003\right)\)
hay \(x\in\left\{2003;-2003\right\}\)
LA
21 tháng 12 2017
a) ĐKXĐ \(\hept{\begin{cases}x-1\ne0\\x+1\ne0\\x\ne0\end{cases}}\Rightarrow\hept{\begin{cases}x\ne1\\x\ne-1\\x\ne0\end{cases}}\)
b)\(\left(\frac{x+1}{x-1}-\frac{x-1}{x+1}+\frac{x^2-4x-1}{x^2-1}\right)\frac{x+2003}{x}\)
\(=\frac{\left(x+1\right)^2-\left(x-1\right)^2+x^2-4x-1}{\left(x-1\right).\left(x+1\right)}.\frac{x+2003}{x}\)
\(\frac{\left(x+1-x+1\right)\left(x+1+x-1\right)+x^2-4x-1}{\left(x-1\right)\left(x+1\right)}.\frac{x+2003}{x}\)
\(\frac{4x+x^2-4x-1}{\left(x-1\right)\left(x+1\right)}.\frac{x+2003}{x}\)
\(=\frac{x^2-1}{\left(x-1\right)\left(x+1\right)}.\frac{x+2003}{x}=\frac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}.\frac{x+2003}{x}\)
\(=\frac{x+2003}{x}\)
20 tháng 11 2018
c) Ta có \(K=\frac{x+2003}{x}\)
Để K nguyên thì x + 2003 ⋮ x
Ta có x ⋮ x => 2003 ⋮ x
=> x thuộc Ư(2003) = { 1; -1; 2003; -2003 }
Vậy khi x thuộc { 1; -1; 2003; -2003 } thì K nguyên
28 tháng 8 2015
a)ĐKXĐ:
\(x-1\ne0;x+1\ne0;x\ne0\)
\(\Leftrightarrow x\ne1;x\ne-1;x\ne0\)
b)\(K=\left(\frac{x+1}{x-1}-\frac{x-1}{x+1}+\frac{x^2-4x-1}{x^2-1}\right).\frac{x+2003}{x}\)
\(=\left(\frac{x+1}{x-1}-\frac{x-1}{x+1}+\frac{x^2-4x-1}{\left(x-1\right)\left(x+1\right)}\right).\frac{x+2003}{x}\)
\(=\left(\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\frac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}+\frac{x^2-4x-1}{\left(x-1\right)\left(x+1\right)}\right).\frac{x+2003}{x}\)
\(=\frac{x^2+2x+1+x^2-2x+1+x^2-4x-1}{\left(x-1\right)\left(x+1\right)}.\frac{x+2003}{x}\)
\(=\frac{3x^2-4x+1}{\left(x-1\right)\left(x+1\right)}.\frac{x+2003}{x}\)
\(=\frac{3x^2-3x-x+1}{\left(x-1\right)\left(x+1\right)}.\frac{x+2003}{x}\)
\(=\frac{3x.\left(x-1\right)-\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}.\frac{x+2003}{x}\)
\(=\frac{\left(x-1\right)\left(3x-1\right)}{\left(x-1\right)\left(x+1\right)}.\frac{x+2003}{x}\)
\(=\frac{\left(3x-1\right)\left(x+2003\right)}{\left(x+1\right).x}\)
\(=\frac{3x^2+6008x-2003}{x^2+x}\)
câu c bí
24 tháng 4 2023
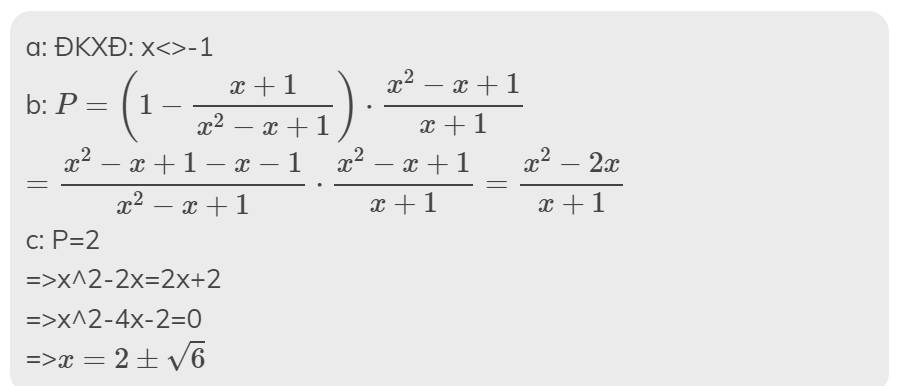
a: ĐKXĐ: x<>-1
b: \(P=\left(1-\dfrac{x+1}{x^2-x+1}\right)\cdot\dfrac{x^2-x+1}{x+1}\)
\(=\dfrac{x^2-x+1-x-1}{x^2-x+1}\cdot\dfrac{x^2-x+1}{x+1}=\dfrac{x^2-2x}{x+1}\)
c: P=2
=>x^2-2x=2x+2
=>x^2-4x-2=0
=>\(x=2\pm\sqrt{6}\)
RR
18 tháng 5 2018
Bài 1 : Điều kiện xác định : \(x\ne\pm1\)
\(K=\left(\frac{x+1}{\left(x-1\right)\left(x+1\right)}-\frac{x-1}{\left(x-1\right)\left(x+1\right)}\right).\frac{x^2-1}{x^2}\)
\(K=\frac{2}{\left(x-1\right)\left(x+1\right)}.\frac{\left(x-1\right)\left(x+1\right)}{x^2}=\frac{2}{x^2}\)
Nhận thấy giá trị của x càng tăng thì giá trị của M càng giảm
mặt khác , giá trị của x lại không giảm quá 0 nên ta không thể nào xác định được giá trị lớn nhất của K