tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = ( x +3 )( 5 - x ) với -3<= x <=5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
3 tháng 8 2017
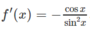
f′(x) < 0 nên và f’(x) > 0 trên ( π /2; 5 π /6] nên hàm số đạt cực tiểu tại x = π /2 và f CT = f( π /2) = 1
Mặt khác, f( π /3) = 2 3 , f(5 π /6) = 2
Vậy min f(x) = 1; max f(x) = 2
CM
18 tháng 4 2019
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
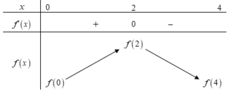
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
QA
1
3 tháng 2 2021
ĐKXĐ : \(-1\le x\le3\)
- ADbu nhi : \(\left(\sqrt{x+1}+\sqrt{3-x}\right)^2\le\left(1^2+1^2\right)\left(\left(\sqrt{x+1}\right)^2+\left(\sqrt{3-x}\right)^2\right)\)
\(=2\left(x+1+3-x\right)=2.4=8\)
\(\Rightarrow\sqrt{x+1}+\sqrt{3-x}\le\sqrt{8}=2\sqrt{2}\)
- Dấu " = " xảy ra \(\Leftrightarrow\dfrac{1}{\sqrt{x+1}}=\dfrac{1}{\sqrt{3-x}}\)
\(\Leftrightarrow x+1=3-x\)
\(\Leftrightarrow x=1\left(TM\right)\)
\(\Rightarrow Max_{f\left(x\right)}=2\sqrt{2}\) tại x = 1.
- Có : \(\sqrt{x+1}+\sqrt{3-x}\ge\sqrt{x+1+3-x}=\sqrt{4}=2\)
- Dấu " = " xảy ra <=> x = -1 ( TM )
\(\Rightarrow Min_{f\left(x\right)}=2\) tại x = - 1 .
.
.
KN
4 tháng 7 2019
\(C=-\left|x+\frac{4}{7}\right|+\frac{12}{19}\)
Ta có: \(\left|x+\frac{4}{7}\right|\ge0\)nên \(-\left|x+\frac{4}{7}\right|\le0\)
\(\Rightarrow C=-\left|x+\frac{4}{7}\right|+\frac{12}{19}\le\frac{12}{19}\)
\(\Rightarrow C_{max}=\frac{12}{19}\)
(Dấu "="\(\Leftrightarrow x=\frac{-4}{7}\))
KN
4 tháng 7 2019
\(D=\left|x-\frac{5}{7}\right|+\frac{2}{3}\)
Vì \(\left|x-\frac{5}{7}\right|\ge0\)nên \(D=\left|x-\frac{5}{7}\right|+\frac{2}{3}\ge\frac{2}{3}\)
\(\Rightarrow D_{min}=\frac{2}{3}\)
(Dấu "="\(\Leftrightarrow x=\frac{5}{7}\))
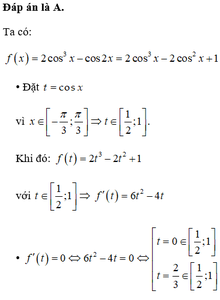
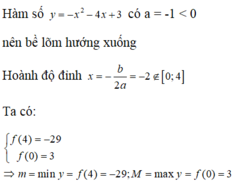
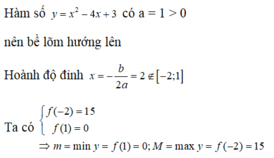
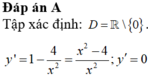
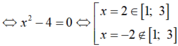
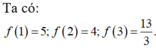
f(x) = -x2 + 2x + 15
Đồ thị hàm số là parabol quay xuống dưới, đỉnh parabol tại điểm (1,16), parabol cắt trục hoành tại 2 điểm có hoành độ là -3 và 5 (bạn tự vẽ hình)
Nhìn vào đồ thị suy ra giá trị lớn nhất của f(x) trong [-3,5] là 16 (khi x = 1) và giá trị nhỏ nhất là 0 (khi x = -3 hoặc x=5)
bạn giúp mình luôn đi