Trong thí nghiệm I-âng về giao thoa ánh sáng. Ánh sáng dùng trong thí nghiệm có 3 loại bức xạ λ1;λ2;λ3 thỏa mãn 16λ1=20λ2=25λ3. Từ vị trí vân sáng bậc 16 đến vân sáng bậc 20 (nằm ở cùng phía so với vân sáng trung tâm) của bức xạ λ2 có số vạch quan sát được là
A. A.7
B. B.12
C. C.11
D. D.8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
Tính ![]()
Đối với vân trùng của 3 hệ vật tính được ![]()
Tính ra 1 vân trùng của λ 1 với λ 2 , 6 vân trùng của λ 2 và λ 3 nên số vân đỏ là Nđ = 13 – 1 – 6 = 6

Đáp án B
+ Khi sử dụng ánh sáng đơn sắc λ 1 và λ 2 , ta thấy giữa hai vân sáng gần nhau nhất cùng màu với vân trung tâm có 6 vân sáng ứng với λ 2 → Nếu ta xét vân đầu tiên trùng giữa hai hệ vân vân trung tâm thì vân thứ hai trùng nhau của hai hệ vân của bức xạ λ 2 ứng với k = 7.
→ Áp dụng điều kiện cho vân sáng trùng nhau của λ 1 và λ 2 → k 1 λ 1 = 7 λ 2 → λ 2 = k 1 . 0 , 56 7 = 0 , 08 k 1 .
+ Dựa vào khoảng giá trị của λ 2 là 0,65 μm < λ 2 < 0,75 μm → λ 2 = 0,72 μm.
+ Khi sử dụng ánh áng thì nghiệm gồm ba bức xạ đơn sắc, trong đó λ 3 = 2 3 λ 2 = 0 , 48 μm.
→ Áp dụng điều kiện trùng nhau của ba hệ vân k 1 λ 1 = k 2 λ 2 = k 3 λ 3 ↔ 7 k 1 = 9 λ 2 = 6 k 3
→ Tại vị trí trùng nhau của ba hệ vân sáng gần vân trung tâm nhất thì
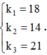
+ Điều kiện trùng nhau của vân sáng của hai bức xạ λ 1 và λ 2 là
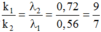
→ Giữa vân trung tâm và vân trùng màu gần vân trung tâm nhất có 1 vị trí trùng giữa vân sáng của λ 1 và λ 2 .
+ Điều kiện trùng nhau của vân sáng của hai bức xạ λ 3 và λ 2 là
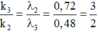
k 3 = 3, 6, 9, 12, 15, 18, 21
k 2 = 2, 4, 6, 8, 10, 12, 14
→ Giữa vân trung tâm và vân trùng màu gần vân trung tâm nhất có 6 vị trí trùng giữa vân sáng của λ 3 và λ 2 .
→ Giữa vân trung tâm và gân trùng màu gần nhất với vân trung tâm có 6 vân sáng đỏ

Chọn B
Ta có i1 = 1,8 mm ứng với λ = 0,6μm.
i12 = 3,6 mm => λ12 = 1,2μm.
Ở đây λ12 chỉ chia hết cho λ = 0,4μm.

Đáp án C.
+ Theo yêu cầu của bài có 4 bức xạ cho vân sáng trùng nhau nên ta có:
![]()
+ Do ánh sáng trắng nên 380nm ≤ λ ≤ 760nm (2)
+ Xét tỷ lệ hai trong bốn bước sóng bài cho: 735/490=3/2
+ Như vậy nếu lấy 4 bức xạ ứng với 4 giá trị k liên tiếp là 2; 3; 4; 5 thì từ (1) tính λ được nhưng vi phạm phương trình (2).
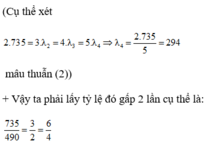
+ Lúc này 4 bức xạ ứng với 4 giá trị k liên tiếp là 4; 5; 6; 7
+ Ta tính được các bước sóng thỏa mãn yêu cầu bài cụ thể là:

+ Tổng bước sóng
![]()
cảu các bức xạ đó là
![]()
=588+420=1008nm





\(N = N_1+N_2+N_2-(N_{12}+N_{13}+N_{23}) -N_{123}\)
Tìm \(N_1,N_2,N_3\)lần lượt là số vân sáng của các bức xạ 1,2,3 trong đoạn x
Số vân sáng của bức xạ 1 trong đoạn x thỏa mãn: \(x_{s2}^{16} \leq x_{1} \leq x_{s2}^{20}\)
=> \(16i_2 \leq k_1i_1 \leq 20i_2\)
=> \(16\frac{\lambda_2}{\lambda_1} \leq k_1 \leq 20\frac{\lambda_2}{\lambda_1}\) (do \(16\lambda_1 = 20\lambda_2 => \frac{\lambda_2}{\lambda_1} = \frac{4}{5}\))
=> \(12,8 \leq k_1 \leq 16 => k_1 = 13,..16.\). Có 4 vân sáng của bức xạ 1.
Làm tương tự: \(16i_2 \leq k_3i_3 \leq 20i_2\) => \(20 \leq k_1 \leq 25 => k_1 = 20,..25.\) Có 6 vân sáng của bức xạ 3.
Trong đoạn x có chứa 5 vân sáng bức xạ 2 vì ((\(k_2 = 16,..20\))
Tìm số vân sáng trùng nhau của bức xạ 1 và bức xạ 2.
\(x_{s2} = x_{s1} => \frac{\lambda_2}{\lambda_1} = \frac{k_1}{k_2} = \frac{4}{5}.\)
Ta có bảng sau:
Như vậy có 1 vân sáng trùng nhau của bức xạ 1 và 2. (\((k_1 ,k_2) = (16,20) \)
Làm tương tự có 1 vân sáng trùng nhau của bức xạ 2 và 3 là \((k_2 ,k_3) = (20,25) \)
1 vân sáng trùng nhau của bức xạ 1 và 3 là \((k_1 ,k_3) = (16,25) \)
Dựa vào các cặp trùng nhau thấy có 1 vị trí trùng nhau của cả 3 bức xạ là \((k_1,k_2 ,k_3) = (16,20,25) \)
Tóm lại, số vân sáng quan sát được trong đoạn x là
\(N = 4+5+6 -(1+1+1)-1 = 11.\)
Chọn đáp án C.11