4, cho tg ABC cân tại A, đường cao ứng vs cạnh bên có độ dài bằng h, góc ở đáy của tg bằng α. CMR: \(S^{_{ABC}}=\dfrac{h^2}{4sin\alpha.cos\alpha}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 6 2017
Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
9 tháng 7 2019
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath
ML
8 tháng 8 2015
Gọi \(h_a;h_b\)là đường cao ứng với cạnh BC và AC.
\(\frac{h_b^2}{\sin\alpha.\cos\alpha}=\frac{\left(\frac{h_b}{\sin\alpha}\right)^2}{\frac{\cos\alpha}{\sin\alpha}}=\frac{\left(\frac{BC\sin\alpha}{\sin\alpha}\right)^2}{\cot\alpha}=\frac{BC}{\cot\alpha}.BC=\frac{2h_a\cot\alpha}{\cot\alpha}.BC\)
\(=2h_a.BC=4.\frac{1}{2}h_a.BC=4S_{ABC}\)
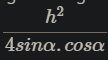
Mình không có bút ở đây nên gợi ý cho bạn xíu xíu nhé.
Lấy M đối xứng với C qua A => MC = 2 AC = 2 AB
=> MBA vuông tại B
Kẻ BH vuông góc AC tại H => BH = h
Ta có sin a . cos a = BH . HC / BC^2 = h . HC / BC^2
=> h^2 / 4 sin a cos a = h.BC^2 / 4HC
Ta phải chứng minh S ABC = h^2 / 4 sin a cos a
<=> BH .AC /2 = h.BC^2 / 4HC
<=> 2 AC .HC= BC^2
<=> CM . HC = BC^2 (hệ thức lượng)