Biết đồ thị hàm số
y =ax+B
song song với đồ thị hàm số
y=x
và đi qua điểm
A(1;3)
. Tìm b?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Thay x=2 và y=3 vào (d), ta được:
4a-6=3
hay a=9/4


a) Đồ thị hàm số đi qua điểm E(-3;2)
\(\Rightarrow2=m\left(2.-3+3\right)+m-1\)
\(\Leftrightarrow m=-\dfrac{3}{2}\)
Vậy...
b) Đồ thị hàm số cắt trục tung tại điểm có tung độ là -5
\(\Rightarrow x=0;y=-5\) thay vào hàm số ta được:
\(-5=m\left(2.0+3\right)+m-1\)\(\Leftrightarrow m=-1\)
Vậy...
c) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 3
\(\Rightarrow x=3;y=0\) thay vào hàm số ta được:
\(0=m\left(2.3+3\right)+m-1\)
\(\Leftrightarrow m=\dfrac{1}{10}\)
Vậy...

\(y=ax^2+2\left(a-2\right)x-3a+1\)
\(=ax^2+2ax-4x-3a+1\)
\(=a\left(x^2+2x-3\right)-4x+1\)
Để mọi giá trị của a đồ thị luôn đi qua 2 điểm thì hàm số trên không phụ thuộc vào nên
\(x^2+2x-3=0\)
\(\leftrightarrow\left(x-1\right)\left(x+3\right)=0\)
\(\rightarrow\orbr{\begin{cases}x=1\\x=-3\end{cases}\rightarrow\orbr{\begin{cases}y=-3\\y=13\end{cases}}}\)
Vậy đồ thị của hàm số trên luôn đi qua 2 điểm có tọa độ \(A\left(1;-3\right),B\left(-3;13\right)\)

Từ đồ thị hàm số f(x) ta thấy đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ x=0;x=1;x=3
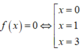
Lại thấy đồ thị hàm số y=f(x) có ba điểm cực trị nên
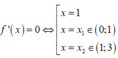
Hàm số y = f x 2 có đạo hàm y'=2f(x).f '(x)
Xét phương trình
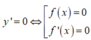
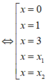
Ta có BXD của y' như sau
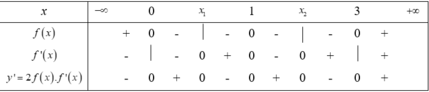
Nhận thấy hàm số y = f x 2 có y' đổi dấu từ âm sang dương tại ba điểm x=0;x=1;x=3 nên hàm số có ba điểm cực tiểu. Và y' đổi dấu từ dương sang âm tại hai điểm x = x 1 ; x = x 2 nên hàm số có hai điểm cực đại.
Chọn đáp án D.