tìm m để giá trị nhỏ nhất của hàm số y=x2-2mx+1 trên [0;1] bằng 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 3 2018
TXĐ: D = R ∖ 2 m
y ' = - x 2 + 4 m x - m 2 x - 2 m 2 = f x x - 2 m 2
Đặt t = x - 1. Khi đó bất phương trình f x ≤ 0 trở thành g t = - t 2 - 2 1 + 2 m t - m 2 + 4 m - 1 ≤ 0
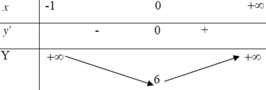
Hàm số nghịch biến trên 1 ; + ∞ khi và chỉ khi
y ' ≤ 0 , ∀ x ∈ 1 ; + ∞ ⇔ 2 m < 1 g t ≤ 0 , ∀ t > 0 * * ⇔ ∆ ' = 0 ∆ ' = 0 S < 0 P ≥ 0 ⇔ m = 0 m ≠ 0 4 m - 2 < 0 m 2 - 4 m + 1 ≥ 0 ⇔ m ≤ 2 - 3
Vậy m ≤ 2 - 3
Đáp án C
CM
15 tháng 9 2018
y = x 2 + 2 x + m - 4 = ( x + 1 ) 2 + m - 5
Ta có ( x + 1 ) 2 + m - 5 ∈ m - 5 ; m - 1
Giá trị lớn nhất của hàm số y = x 2 + 2 x + m - 4 trên đoạn[ -2; 1] đạt giá trị nhỏ nhất khi
m - 5 < 0 m - 1 > 0 5 - m = m - 1 ⇔ m = 3
Chọn B.
CM
18 tháng 1 2018
Chọn đáp án D
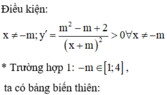
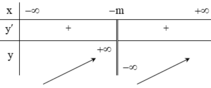
Vậy có đúng 1 giá trị của thỏa mãn điều kiện bài ra.
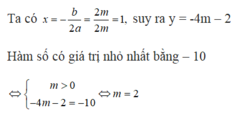
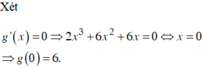
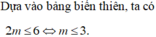
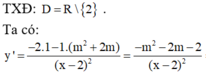
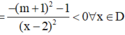
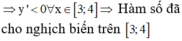
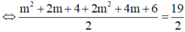
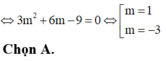
\(y=x^2-2mx+1=\left(x-m\right)^2+1-m^2\)
=> Tọa độ đỉnh là \(I\left(m;1-m^2\right)\)
Do a=1>0 => Đồ thị hàm số có bề lõm hướng lên trên
=> H/s đồng biến trong khoảng \(\left(m;+\infty\right)\)
H/s nghịch biến trong khoảng \(\left(-\infty;m\right)\)
TH1: \(\left[0;1\right]\in\left(m;+\infty\right)\Rightarrow y_{min}=y\left(0\right)=1\left(loại\right)\)
TH2: \(\left[0;1\right]\in\left(-\infty;m\right)\Rightarrow y_{min}=y\left(1\right)=2-2m=3\Leftrightarrow m=-\frac{1}{2}\)
Mà \(\left[0;1\right]\notin\left(-\infty;-\frac{1}{2}\right)\)=> Loại
TH3: \(m\in\left[0;1\right]\Rightarrow y_{min}=y\left(m\right)=m^2-2m.m+1=-m^2+1=3\left(vo nghiem\right)\)
Vậy không có giá trị m thỏa mãn đề bài