HELP MEEEEEE !!!
Cho ΔBC cân tại A ( Â<40°) có BM, CN là 2 đường phân giác của ΔABC
A) chứng minh BCMN là hình thang cân
B) BE, CF là 2 đường cao của ΔABC. Chứng minh EMNF là hình thang cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CC
4 tháng 9 2018
vì tam giác ABC cân tại A (gt)
góc ABC=gócACB
=>\(\frac{ABC}{2}\)=\(\frac{ACB}{2}\)
=>\(\widehat{B_1}\)=\(\widehat{B_2}\)=\(\widehat{C_1}\)=\(\widehat{C_2}\)
(vì CN là phân giác \(\widehat{ACB}\):BM là phân giác \(\widehat{ABC}\))
xét tam giác ABM và tam giác ACN có
\(\widehat{B_1}\)=\(\widehat{C_1}\)
 chung
AB=AC(2 cạnh bên)
Do đó tam giác ABM=tam giác ACN(g.c.g)
=>AN=AM
=>tam giác AMN cân tại A
phần a thui mik nghĩ 2 phần còn lại đã
11 tháng 4 2023
ΔACK vuông tại C có CI vuông góc AK
nên AK*AI=AC^2
ΔCAB vuông tại C có CO là đường cao
nên AO*AB=AC^2=AK*AI
HA
1
13 tháng 3 2023
a: góc B=góc C=(180-80)/2=50 độ
b: góc A=180-2*65=50 độ
LC
3
LB
9 tháng 5 2017
Ta có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{A}=180^o-\left(\widehat{B}+\widehat{C}\right)\)
Vì trong tam giác cân, hai góc kề một đáy bằng nhau
\(\Rightarrow\widehat{B}=\widehat{C}=70^o\)
\(\Rightarrow\widehat{A}=180^o-\left(70^o+70^o\right)=180^o-140^o=40^o\)
Vậy \(\widehat{A}=40^o\)
9 tháng 5 2017
Ta có: tam giácABC cân tại A
->góc B =góc C(T/C của tam giác cân)
mà góc B =70o
->Góc C =góc B=70o
Ta có :
góc A +góc B +góc C=180o(đ/l tổng 3 góc của một tam giác)
->góc A=180o-(góc B + góc C)
=180O - (70O X 2)
=40O
=>góc A =40O
CH
Cô Hoàng Huyền
Admin
VIP
14 tháng 3 2018
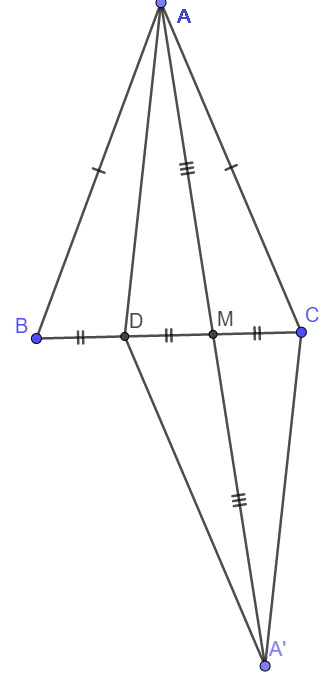
Gọi M là trung điểm DC và A' là điểm thuộc tia AM sao cho AM = MA'.
Khi đó ta thấy ngay \(\Delta AMC=\Delta A'MD\left(c-g-c\right)\)
\(\Rightarrow\widehat{MAC}=\widehat{MA'D}\) và AC = A'D.
Ta cũng có ngay \(\Delta ABD=\Delta ACM\left(c-g-c\right)\Rightarrow\widehat{BAD}=\widehat{CAM}\) và AB = AC
Kẻ AH vuông góc BC. Do tam giác ABC cân nên AH đồng thời là trung tuyến.
Vậy thì ta thấy ngay DH < BH nên theo quan hệ giữa đường xiên và hình chiếu ta có AD < AB
Suy ra AD < AC hay AD < DA'
Xét tam giác ADA' có AD < DA' nên theo quan hệ giữa cạnh và góc trong tam giác ta có :
\(\widehat{DAM}>\widehat{DA'M}\Rightarrow\widehat{DAM}>\widehat{MAC}\)
Lại có \(\widehat{DAM}+\widehat{MAC}=\widehat{CAD}\) nên \(\widehat{MAC}< \frac{1}{2}\widehat{CAD}\)
Vậy thì \(\widehat{BAD}< \frac{1}{2}\widehat{CAD}\left(đpcm\right)\)
Tham khảo :P http://lazi.vn/edu/exercise/cho-tam-giac-abc-can-tai-a-a-40-co-bm-cn-la-2-duong-phan-giac-chung-minh-bcmn-la-hinh-thang-can