Cho tứ giác ABCD gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh (AB+BC+CD+DA)/2<AC +BD.
CÁC BN GIÚP MIK VS NHEN!!! THANK YOU NHÌU NHÌU!!!>3<!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

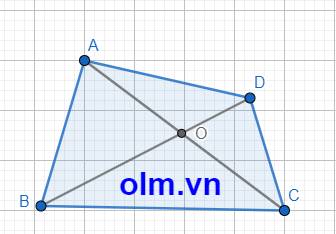
Xét \(\Delta\)AOD ta có: AO + OD > AD (trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét \(\Delta\) OCD ta có: BO + OC > BC ( trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AO + OD + BO + OC > AD + BC
(AO + OC) + ( OD + OB > AD + BC
AC+ BD > AD + BC
Chứng Minh tương tự ta có: AC + BD > AB + CD

a) Ta có:-
- M là trung điểm của AB
⇒ AM = MB.
- N là trung điểm của BC
⇒ BN = NC.
- P là trung điểm của CD
⇒ CP = PD.
- Q là trung điểm của DA
⇒ DQ = QA.
Do đó, ta có: AM = MB = BN = NC = CP = PD = DQ = QA.
⇒ tứ giác MNPQ là hình bình hành.
Có:
- I là trung điểm của AC
⇒AI = IC.
- K là trung điểm của BD
⇒ BK = KD.
Do đó, ta có: AI = IC = BK = KD.
⇒ tứ giác INKQ là hình bình hành.
b)Gọi O là giao điểm của MP và NQ ta có:
MP // AB và NQ//CD ( M và N là trung điểm của AB và CD).
⇒ MP song song với NQ.
do đó :O nằm trên MP và NQ.
Gọi H là giao điểm của MI và NK ta có:
MI // AC và NK // BD (do I và K là trung điểm của đường chéo AC và BD).
⇒ MI song song với NK.
Do đó: H nằm trên cả MI và NK.
Gọi G là giao điểm của OH và BD ta có:
OH //MP và BD // MP (do O nằm trên MP và NQ, và H nằm trên MI và NK).
⇒ OH song song với BD.
doo đó: G nằm trên OH và BD.
⇒ I, O, K thẳng hàng.(ĐPCM)
a: Xét ΔBAC có BM/BA=BN/BC=1/2
nên MN//AC và MN=1/2AC
Xét ΔDAC có DQ/DA=DP/DC
nên PQ//AC và PQ/AC=DQ/DA=1/2
=>PQ=1/2AC
=>MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔCAB có CI/CA=CN/CB=1/2
nên IN//AB và IN=1/2AB
Xét ΔDAB có DQ/DA=DK/DB=1/2
nên QK//AB và QK=1/2AB
=>IN//QK và IN=QK
=>INKQ là hình bình hành
b: MNPQ là hình bình hành
=>MP cắt NQ tại trung điểm của mỗi đường
=>O là trung điểm của NQ
INKQ là hbh
=>IK cắt NQ tại trung điểm của mỗi đường
=>I,O,K thẳng hàng

a)
Ta có
OA + OB > AB ( Bất đẳng thức tam giác )
OC + OD > CD ( Bất đẳng thức tam giác )
Công dọc theo vế:
=> OA + OB + OC +OD > AB + CD
=> AC + BD > AB + CD
Bài toán được chứng minh
b)
Ta có:
OA + OD > AD ( Bất đẳng thức tam giác )
OC + OB > CB ( Bất đẳng thức tam giác )
Công dọc theo vế:
=> OA + OD + OC + OB > AD + CB
=> AC + BD > AD + BC
Bài toán được chứng minh

Xét tam giác ABD:
E là trung điểm AB (gt).
H là trung điểm AD (gt).
\(\Rightarrow\) EH là đường trung bình.
\(\Rightarrow\) EH // BD; EH = \(\dfrac{1}{2}\) BD (Tính chất đường trung bình). (1)
Xét tam giác CBD:
F là trung điểm BC (gt).
G là trung điểm CD (gt).
\(\Rightarrow\) FG là đường trung bình.
\(\Rightarrow\) FG // BD; FG = \(\dfrac{1}{2}\) BD (Tính chất đường trung bình). (2)
Xét tamgiacs ACD:
H là trung điểm AD (gt).
G là trung điểm CD (gt).
\(\Rightarrow\) HG là đường trung bình.
\(\Rightarrow\) HG // AC (Tính chất đường trung bình).
Mà AC \(\perp\) BD (Tứ giác ABCD là hình thoi).
\(\Rightarrow\) HG \(\perp\) BD.
Lại có: EH // BD (cmt).
\(\Rightarrow\) EH \(\perp\) HG.
Từ (1) và (2) \(\Rightarrow\) EH // FG; EH = FG.
\(\Rightarrow\) Tứ giác EFGH là hình bình hành (dhnb).
Mà EH \(\perp\) HG (cmt).
\(\Rightarrow\) Tứ giác EFGH là hình chữ nhật (dhnb).
b) Tứ giác ABCD là hình thoi (gt).
\(\Rightarrow\) AC cắt BD tại trung điểm mỗi đường (Tính chất hình thoi).
Mà I là giao điểm của AC và BD (gt.)
\(\Rightarrow\) I là trung điểm của AC và BD.
\(\Rightarrow\left\{{}\begin{matrix}AI=\dfrac{1}{2}AC=\dfrac{1}{2}.8=4\left(cm\right).\\IB=\dfrac{1}{2}BD=\dfrac{1}{2}.10=5\left(cm\right).\end{matrix}\right.\)
Xét tam giác ABI: AI \(\perp\) BI (AC \(\perp\) BD).
\(\Rightarrow\) Tam giác ABI vuông tại I.
\(\Rightarrow S_{\Delta ABI}=\dfrac{1}{2}AI.IB=\dfrac{1}{2}.4.5=10\left(cm^2\right).\)
\(\perp\)

Câu 15:
a: Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình
=>EH//BD và EH=BD/2(1)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của CD
Do đó: FG là đường trung bình
=>FG//BD và FG=BD/2(2)
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình
=>EF//AC
=>EF⊥BD
=>EF⊥EH
Từ (1) và (2) suy ra EH//FG và EH=FG
hay EHGF là hình bình hành
mà EF⊥EH
nên EHGF là hình chữ nhật
b: AI=AC/2=8/2=4(cm)
BI=BD/2=10/2=5(cm)
\(S_{AIB}=\dfrac{AI\cdot BI}{2}=\dfrac{5\cdot4}{2}=10\left(cm^2\right)\)

Gọi O là giao điểm hai đường chéo AC và BD
\(OA+OB>AB\) ; \(OB+OC>BC\) ; \(OC+OD>CD\) ; \(OA+OD>AD\)
Cộng các bất đẳng thức trên theo vế được : \(2\left(OA+OB+OC+OD\right)>AB+BC+CD+AD\)
\(\Rightarrow2\left(AC+BD\right)>AB+BC+CD+AD\) \(\Rightarrow AC+BD>\frac{AB+BC+CD+DA}{2}\) (1)
\(AD+CD>AC\) ; \(BC+CD>BD\) ; \(AB+BC>AC\) ; \(AB+AD>BD\)
Cộng các bất đẳng thức trên theo vế được : \(2\left(AC+BD\right)< 2\left(AB+BC+CD+DA\right)\)
\(\Rightarrow AC+BD< AB+BC+CD+DA\)(2)
Từ (1) và (2) ta có : \(\frac{AB+BC+CD+DA}{2}< AC+BD< AB+BC+CD+AD\)
hay \(\frac{AB+BC+CD+DA}{2}< OA+OB+OC+OD< AB+BC+CD+AD\)

a) Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và \(QP=\dfrac{AC}{2}\)(2)
Từ (1) và (2) suy ra MN//QP và MN=QP
Xét tứ giác MNPQ có
MN//QP(cmt)
MN=QP(cmt)
Do đó: MNPQ là hình bình hành
Xét ΔABD có
Q là trung điểm của AD
M là trung điểm của AB
Do đó: QM là đường trung bình của ΔABD
Suy ra: QM//DB và \(QM=\dfrac{DB}{2}\)
hay \(QM=\dfrac{AC}{2}\)(3)
Từ (2) và (3) suy ra QM=QP
Hình bình hành MNPQ có QM=QP(cmt)
nên MNPQ là hình thoi

a: Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy a MQ//NP và MQ=NP
=>MNPQ là hình bình hành
b: Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2 và MN//AC
Để MNPQ là hình chữ nhật thì MN vuông góc với MQ
=>AC vuông góc với BD
Theo bất đẳng thức tam giác ta có:
OA + OB > AB
OB + OC > BC
OC + OD > CD
OD + OA > DA
Cộng 4 bđt trên theo vế ta được:
2(OA + OB + OC + OD) > AB + BC + CD + DA
<=> (OA + OC) + (OB + OD) > (AB + BC + CD + DA)/2
\(\Leftrightarrow AC+BD>\frac{AB+BC+CD+DA}{2}\)