Cho a>0, b>0, a + 2b = 1. Chứng minh
1÷8ab + 2ab ÷ a2 + 4b2 >= 3÷2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
0
TB
22 tháng 4 2019
\(A=\frac{2ab}{4ab}+\frac{2ab}{a^2+4b^2}+\frac{1}{8ab}-\frac{1}{2}\)
áp dụng bđt AM-GM , a,b> 0
\(\Rightarrow A\ge2ab\left(\frac{4}{4ab+a^2+4b^2}\right)+\frac{1}{8ab}-\frac{1}{2}\)
\(\Rightarrow A\ge\frac{8ab}{1}+\frac{1}{8ab}-\frac{1}{2}\)
\(\Rightarrow A\ge2-\frac{1}{2}=\frac{3}{2}\)
AH
Akai Haruma
Giáo viên
13 tháng 12 2023
A.
$a^2+4b^2+9c^2=2ab+6bc+3ac$
$\Leftrightarrow a^2+4b^2+9c^2-2ab-6bc-3ac=0$
$\Leftrightarrow 2a^2+8b^2+18c^2-4ab-12bc-6ac=0$
$\Leftrightarrow (a^2+4b^2-4ab)+(a^2+9c^2-6ac)+(4b^2+9c^2-12bc)=0$
$\Leftrightarrow (a-2b)^2+(a-3c)^2+(2b-3c)^2=0$
$\Rightarrow a-2b=a-3c=2b-3c=0$
$\Rightarrow A=(0+1)^{2022}+(0-1)^{2023}+(0+1)^{2024}=1+(-1)+1=1$
AH
Akai Haruma
Giáo viên
13 tháng 12 2023
B.
$x^2+2xy+6x+6y+2y^2+8=0$
$\Leftrightarrow (x^2+2xy+y^2)+y^2+6x+6y+8=0$
$\Leftrightarrow (x+y)^2+6(x+y)+9+y^2-1=0$
$\Leftrightarrow (x+y+3)^2=1-y^2\leq 1$ (do $y^2\geq 0$ với mọi $y$)
$\Rightarrow -1\leq x+y+3\leq 1$
$\Rightarrow -4\leq x+y\leq -2$
$\Rightarrow 2020\leq x+y+2024\leq 2022$
$\Rightarrow A_{\min}=2020; A_{\max}=2022$
TG
10 tháng 8 2021
\(\dfrac{1}{a-2b}.\sqrt{b^2\left(a^2-4ab+4b^2\right)}=\dfrac{1}{a-2b}.b.\left|a-2b\right|=\dfrac{1}{a-2b}.b.\left(2b-a\right)=-b\)
10 tháng 8 2021
\(\dfrac{1}{a-2b}\cdot\sqrt{b^2\cdot\left(a^2-4ab+b^2\right)}\)
\(=\dfrac{1\cdot\left(a-2b\right)}{a-2b}\cdot b\)
=b
TH
1
OP
8 tháng 8 2016
a + 2b = 1 => 2b = 1 - a
Biến đổi VT:
\(a^3+8b^3+2ab-a^2-4b^2\)
\(=a\left(a^2+2b-a\right)+\left(2b\right)^3-\left(2b\right)^2\)
\(=a\left(a^2+1-a-a\right)+\left(2b\right)^2\left(2b-1\right)\)
\(=a\left(a^2-2a+1\right)+\left(1-a\right)^2\left(1-a-1\right)\)
\(=a\left(a-1\right)^2-a\left(1-a\right)^2\)
\(=a\left[\left(a-1\right)^2-\left(1-a\right)^2\right]\)
\(=a\left(a-1+1-a\right)\left(a-1-1+a\right)\)
\(=0\)(đpcm)
CM
24 tháng 1 2019
a) Biến đổi vế trái:
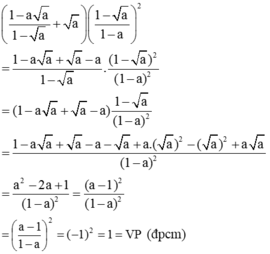
b) Biến đổi vế trái:
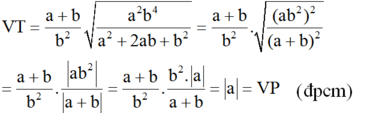
( v ì a + b > 0 n ê n | a + b | = a + b ; b 2 > 0 )
CM
30 tháng 10 2019
Ta có a 2 + 4 b 2 = 12 a b ⇔ a + 2 b 2 = 16 a b
Suy ra
2 log 3 a + 2 b = log 3 2 4 + log 3 a + log 3 b ⇔ log 3 a + 2 b = 2 log 3 2 + 1 2 log 3 a + log 3 b
Do đó cả hai mệnh đề đều sai
Đáp án C