Cho đường tròn tâm O bán kính OM. Dây AB của đường tròn vuông góc OM tại trung điểm của OM. Tính OM khi AB = \(6\sqrt{3}cm\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2 nếu ai giải được thì làm ơn gửi cho mình cách giải nhé!!Mình cũng có bài này mà ko giải được

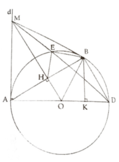
a, Tính được AH = 5 . Từ đó suy ra AB= 2 5 và OM=4,5cm
b, Với ∆MAB cân tại MH là trung tuyến vừa là đường cao;
Ta có ∆MAO = ∆MBO => MBOB => MB là tiếp tuyến của (O)
c, Dễ thấy M A 2 = M H . M O (Theo hệ thức lượng trong tam giác vuông)
Chứng minh được: ∆MBE:∆MBD
=> M B 2 = M E . M D = M A 2
=> MH.MO = ME.MD
=> ∆EHM:∆ODM (c.g.c)
=> E H M ^ = O D M ^
d, Kẻ BK ⊥ AD
Ta có: S H O A = 1 2 S A B D = 1 4 B K . A D
Vì BK ≤ 3 => S H O A lớn nhất khi B là điểm chính giữa cung AD khi đó AM = OA = 3

1: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
2: ΔOAB cân tại O
mà OM là đường cao
nên M là trung điểm của AB
ΔOAC cân tại O
mà ON là đường cao
nên N là trung điểm của AC
=>NM là đừog trung bình
=>MN//BC
=>MN//AE
=>AMNE là hình thang cân
=>AM=EN; AN=EM
ΔAHB vuông tại H có HM là trung tuyến
nên HM=AB/2=MA=MB
ΔHAC vuông tại H có HN là trung tuyến
nên HN=AN=CN=AC/2
=>HM=EN; HN=EM
=>HMEN là hình bbình hành
=>K làtrung điểm của MN
=>IK vuông góc MN
=>IK vuông góc BC
3: goc MDE+gó MDH=180 độ
=>góc MDE=góc MBH
=>BMDH nội tiếp
=>góc MDB=góc MHB=góc MBH
=>góc MDB=góc MDE
=>DM là phân giác của góc BDE

1: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
2: Gọi giao EO và BC là P
AE//BC
AE vuông góc OE
=>OE vuông góc BC
=>OP vuông góc BC
=>P là trung điểm của BC
AEPH là hình chữ nhật
=>AE=PH
EJ giao BC=J
=>AE=JC
=>JC=HP
=>HJ=PC=BC/2=MN
=>HMNJ là hình bình hành
=>HM//NJ và HM=NJ
=>HM//EN và HM=EN
=>EMHN là hbh
=>K là trung điểm của MN
=>IK vuông góc MN
=>IK vuông góc BC