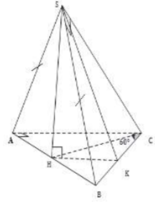
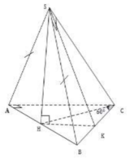
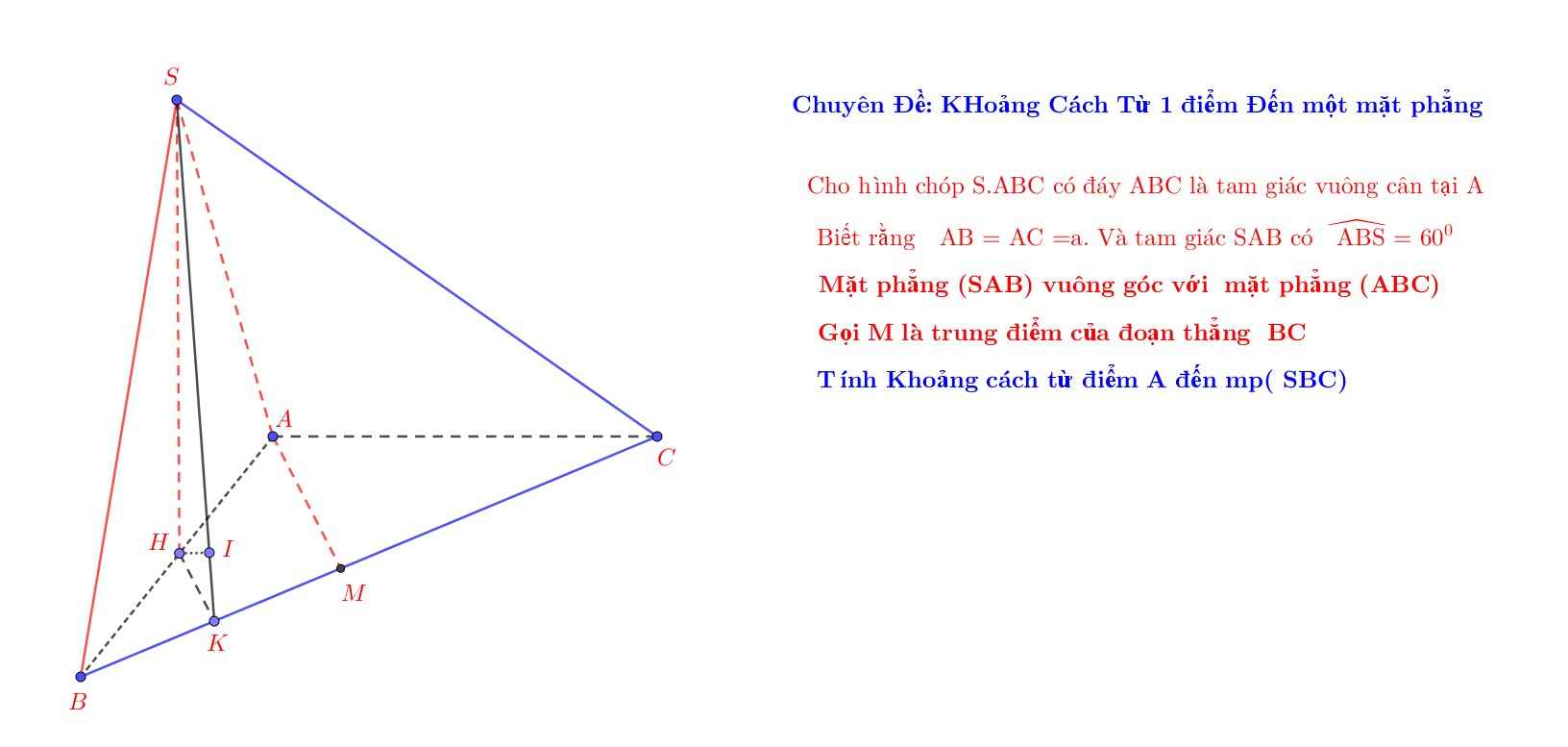
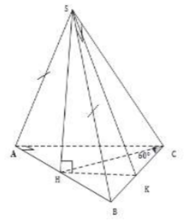
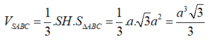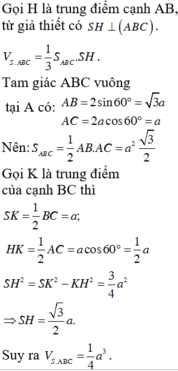cho hình chóp SABC có tam giác ABC vuông cân tại A, AB=a, tam giác SAB cân tại S. (SAB) vuông góc với (ABC). (SBC) tạo với đáy 1 góc 45°. Tính thể tích SABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BN
18 tháng 4 2016
chứng minh được AH=BH -> SA= SB _> tam giác SAB cân ở S
gọi M là trung điểm của AB -> SM vuông góc với AB -> góc giữa mp (SAB) và mp (ABC) là góc SMH -> góc SMH = 60 độ
-> tìm được SH -> tìm được thể tích
tìm diên tích tam giác SAB -> khoảng cách từ C đến mp (SAB)
Vì I là trung điểm của SC nên khoảng cách từ I đến mp (SAB) bằng một nửa khoảng cách từ C đến mp (SAB)
DT
21 tháng 5 2022
Hình bạn tự vẽ nha mình biếng á chứ khog có j đou=)
Ta có : \(\left\{{}\begin{matrix}CA\perp AB\\\left(ABC\right)\perp\left(SAB\right)\\\left(ABC\right)\cap\left(SAB\right)=AB\end{matrix}\right.\) \(\Rightarrow CA\perp\left(SAB\right)\)
Kẻ \(AK\perp SB\) và \(AH\perp CK\) tại H.
Ta có : \(\left\{{}\begin{matrix}SB\perp AK\\SB\perp CA\end{matrix}\right.\) \(\Rightarrow SB\perp\left(ACK\right)\Rightarrow SB\perp AH\)
Do : \(\left\{{}\begin{matrix}AH\perp CK\\AH\perp SB\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\Rightarrow d\left(A;\left(SBC\right)\right)=AH\)
Xét t/g ABK , ta có : AK = AB
=> \(sin\widehat{ABK}=\alpha sin60^o=\dfrac{a\sqrt{3}}{2}\)
Xét t/g ACK , ta có : \(\dfrac{1}{AH^2}=\dfrac{1}{AK^2}+\dfrac{1}{AC^2}=\dfrac{7}{3a^2}\Rightarrow AH=\dfrac{a\sqrt{21}}{7}\)
CM
23 tháng 10 2019
Đáp án là A
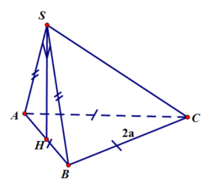
Ta có :
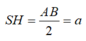
( Do SAB là tam giác vuông cân tại S cạnh huyền AB=2a)
Diện tích tam giác ABC là
Vậy thể tích khối chóp SABC là:
