Cho tam giác ABC , các đường phân giác AB , BE , CF gặp nhau tại I .
a, Tính \(\widehat{IAC}+\widehat{IBC}+\widehat{ICA}\)
b, Kẻ IH vuông góc với BC tại H . CMR : \(\widehat{BIH}=\widehat{CID}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
1 tháng 4 2017
Mình chỉ giải được phần a) thôi
a) BE là phân giác của góc ABC
=>EBC=EBA=1/2ABC (1)
CF là phân giác của góc ACB
=>ACF=BCF=1/2ACB (2)
ADlà phân giác của góc BAC
=>BAD=CAD=1/2BAC (3)
Từ (1), (2), (3) ta có
1/2ABC+1/2ACB+1/2BAC=1/2(ABC+ACB+BAC)=1/2.180=90
Hay IAC+IBC+ICA=90
17 tháng 9 2023
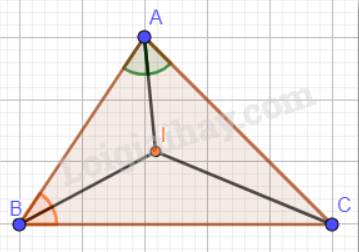
Ta có: I là giao điểm của hai đường phân giác góc A và góc B nên suy ra: CI là đường phân giác của góc C.
Vậy \(\widehat {ICA} = \widehat {ICB}\) ( tính chất tia phân giác của một góc).
Đáp án: A. \(\widehat {ICA} = \widehat {ICB}\).
14 tháng 12 2019
a) Xét \(\Delta AMB\)và \(\Delta AMC\)có:
AB = AC (gt)
\(\widehat{BAM}=\widehat{CAM}\)(AM là tia phần giác của góc A)
AM là cạnh chung
\(\Rightarrow\Delta AMB=\Delta AMC\left(c.g.c\right)\)
b) Ta có: \(\Delta AMB=\Delta AMC\)(theo a)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}\)(2 góc tương ứng)
Mà \(\widehat{AMB}+\widehat{AMC}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=90^o\)
\(\Rightarrow AM\perp BC\)
Lại có: \(IH\perp BC\Rightarrow AM//IH\)
\(\Rightarrow\widehat{BIH}=\widehat{BAM}\)(2 gó so le trong)
Mà \(\widehat{BAM}=\frac{1}{2}\cdot\widehat{BAC}\)(AM là tia p/g của góc A)
\(\Rightarrow\widehat{BIH}=\frac{1}{2}\cdot\widehat{BAC}\)
hay \(\widehat{BAC}=2\widehat{BIH}\)
17 tháng 9 2023
a) I là giao điểm của ba đường phân giác tại ba góc A, B, C nên:
\(\widehat {IAB} = \widehat {IAC};\widehat {IBA} = \widehat {IBC};\widehat {ICB} = \widehat {ICA}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = 180^\circ \\\widehat {IAB} + \widehat {IAC} + \widehat {IBA} + \widehat {IBC} + \widehat {ICB} + \widehat {ICA} = 180^\circ \\2\widehat {IAB} + 2\widehat {IBC} + 2\widehat {ICA} = 180^\circ \end{array}\)
Vậy \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \).
b) Tổng ba góc trong một tam giác bằng 180°. Xét tam giác BIC:
\(\begin{array}{l}\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ \\\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\end{array}\).
Mà \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \)→ \(\widehat {IBC} + \widehat {ICA} = 90^\circ - \widehat {IAB}\).
Vậy: \(\begin{array}{l}\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\\\widehat {BIC} = 180^\circ - (90^\circ - \widehat {IAB})\\\widehat {BIC} = 90^\circ + \widehat {IAB}\end{array}\)
Mà \(\widehat {IAB} = \dfrac{1}{2}\widehat {BAC}\)(IA là phân giác của góc BAC).
Vậy \(\widehat {BIC} = 90^\circ + \widehat {IAB} = 90^\circ + \dfrac{1}{2}\widehat {BAC}\).
31 tháng 7 2021
a) Ta có: \(\sin\widehat{ACB}=\dfrac{AB}{BC}\)
nên \(AB=\dfrac{3}{5}\cdot20=12\left(cm\right)\)
Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=20^2-12^2=256\)
hay AC=16(cm)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔCBD vuông tại B có BA là đường cao ứng với cạnh huyền CD, ta được:
\(AC\cdot AD=AB^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(BH\cdot BC=AB^2\)(2)
Từ (1) và (2) suy ra \(AC\cdot AD=BH\cdot BC\)