Cho đa thức f(x) = ax2+bx+c. Biết f(1),f(2),f(0) đều có giá trị nguyên.cmr:đa thức trên thuộc Z với mọi x thuộc Z
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Theo giả thiết, ta có:
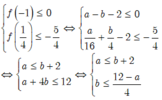
Khi đó 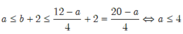
Vậy 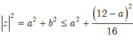
Xét hàm số ![]() với
với ![]() , có
, có ![]()
Tính các giá trị ![]() suy ra
suy ra ![]()
Vậy giá trị lớn nhất của
z
là: ![]()


Ta có f(0)=a.0
2
+b.0+c=c=>c là số nguyên
f(1)=a.1
2
+b.1+c=a+b+c
Vì c là số nguyên=>a+b là số nguyên(1)
f(2)=a.2
2
+b.2+c=2.(2a+b)+c=>2.(2a+b)là số nguyên=>2a+b là số nguyên(2)
Từ (1)và(2)=>(2a+b)-(a+b)=2a+b-a-b=a là số nguyên=>a là số nguyên
Do a+b là số nguyên, mà a là số nguyên
=>b là số nguyên
Vậy f(x) luôn nhận giá trị nguyên với mọi x

Giả sử f(0), f(1), f(2) có giá trị nguyên là m,n,p. Theo đề bài ta có
\(1\hept{\begin{cases}c=m\left(1\right)\\a+b+c=n\left(2\right)\\4a+2b+c=p\left(3\right)\end{cases}}\)
Ta lấy (3) - 2(2) + (1) vế theo vế ta được
2a = p - 2n + m
=> 2a là số nguyên
Ta lấy 4(2) - (3) - 3(1) vế theo vế ta được
2b = 4n - p - 3m
=> 2b cũng là số nguyên

*f(0) nguyên suy ra 0+0+c=c nguyên
*Vì c nguyên và f(1)=a+b+c nguyên suy ra a+b nguyên
*Tương tự vs f(2)=4a+2b+c suy ra 2a nguyên (Vì 4a+2b và 2(a+b) đều nguyên)
Vì 2a và 2(a+b) nguyên suy ra 2b nguyên (đpcm)
Ta có : f(0) = a . 02 + b . 0 + c = c \(\in\)Z
f(1) = a . 12 + b . 1 + c = a + b + c
vì c \(\in\)Z \(\Rightarrow\)a + b \(\in\)Z ( 1 )
f(2) = a . 22 + b . 2 + c = 4a + 2b + c = 2 . ( 2a + b ) + c
vì c \(\in\)Z \(\Rightarrow\)2 . ( 2a + b ) \(\in\)Z \(\Rightarrow\)2a + b \(\in\)Z ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\)( 2a + b ) - ( a + b ) \(\in\) Z \(\Rightarrow\)a \(\in\)Z
\(\Rightarrow\)b \(\in\)Z
Vậy f(x) thuộc Z \(\forall\)x thuộc Z