giúp e bài 4,5 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
a) Xét tứ giác DMEC có
ME//DC(gt)
MD//EC(gt)
Do đó: DMEC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Ta có: CDME là hình bình hành(cmt)
nên Hai đường chéo CM và DE cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà I là trung điểm của DE(gt)
nên I là trung điểm của CM
hay C,M,I thẳng hàng


Bài 5:
f(x) có 1 nghiệm x - 2
=> f (2) = 0
\(\Rightarrow a.2^2-a.2+2=0\)
\(\Rightarrow4a-2a+2=0\)
=> 2a + 2 = 0
=> 2a = -2
=> a = -1
Vậy:....
P/s: Mỗi lần chỉ đc đăng 1 câu hỏi thôi! Bạn vui lòng đăng bài hình trên câu hỏi khác nhé!
a)Ta có △MIP cân tại M nên ˆMNI=ˆMPIMNI^=MPI^
Xét △MIN và △MIP có:
ˆNMI=ˆPMINMI^=PMI^
MI : cạnh chung
ˆMNI=ˆMPIMNI^=MPI^
Nên △MIN = △MIP (c.g.c)
b)Gọi O là giao điểm của EF và MI
Vì △MNP là tam giác cân và MI là đường phân giác của △MIP
Suy ra MI đồng thời là đường cao của △MNP
Nên ˆMOE=ˆMOF=90oMOE^=MOF^=90o
Xét △MOE vuông tại O và △MOF vuông tại O có:
OM : cạnh chung
ˆEMO=ˆFMOEMO^=FMO^(vì MI là đường phân giác của △MIP và O∈∈MI)
Suy ra △MOE = △MOF (cạnh góc vuông – góc nhọn kề)
Nên ME = MF
Vậy △MEF cân
tham khảo



Câu 4:
a) Do mắc nối tiếp nên:
\(R_{tđ}=R_1+R_2=10+10=20\left(\Omega\right)\)
b) Điện trở tương đương của đoạn mạch lúc này là:
\(R_{tđ}=R_1+R_2+R_3=10+10+5=25\left(\Omega\right)\)
Câu 5:
a) Do mắc nối tiếp nên:
\(R_{tđ}=R_1+R_2=3+6=9\left(\Omega\right)\)
b) Cường độ dòng điện qua mỗi điện trở:
\(I=I_1=I_2=\dfrac{U}{R_{tđ}}=\dfrac{12}{9}=\dfrac{4}{3}\left(A\right)\)
c) Hiệu điện thế 2 đầu R1:
\(U_1=I_1.R_1=\dfrac{4}{3}.3=4\left(V\right)\)
Hiệu điện thế 2 đầu R2:
\(U_2=I_2.R_2=\dfrac{4}{3}.6=8\left(V\right)\)
Bài 4 :
a) Điện trở tương đương của đoạn mạch
\(R_{tđ}=R_1+R_2=10+10=20\left(\Omega\right)\)
b) Điện trở tương đương của đoạn mạch lúc này
\(R_{tđ}=R_1+R_2+R_3=10+10+5=25\left(\Omega\right)\)
Chúc bạn học tốt

1 a
2 d
3 b
4 c
5 a
-----------------------
1 c
2 a
3 b
4 d
\(@HMyT\)

Bài 5
a) 1/3 : (x - 1/2) + 5/6 = -3/2
1/3 : (x - 1/2) = -3/2 - 5/6
1/3 : (x - 1/2) = 7/3
x - 1/2 = 1/3 : 7/3
x - 1/2 = 1/7
x = 1/7 + 1/2
x = 3/14
b) (0,16 + 0,01)²x = 0,9
(0,4 + 0,1)²x = 0,9
0,5².x = 0,9
0,25.x = 0,9
x = 0,9 : 0,25
x = 3,6
c) x + (-3/4) : 1 1/8 = 1/3
x - 3/4 : 9/8 = 1/3
x - 2/3 = 1/3
x = 1/3 + 2/3
x = 1
d) (2x - 1)⁴ = 81
(2x - 1)⁴ = 3⁴
2x - 1 = 3 hoặc 2x - 1 = -3
*) 2x - 1 = 3
2x = 4
x = 4 : 2
x = 2
*) 2x - 1 = -3
2x = -2
x = -2 : 2
x = -1
Vậy x = -1; x = 2
Bài 4
a) -1/10 + 2/5 x + 7/20 = 1/10
2/5 x = 1/10 + 1/10 - 7/20
2/5 x = -3/20
x = -3/20 : 2/5
x = -3/8
b) 1/3 + 1/2 : x = -1/5
1/2 : x = -1/5 - 1/3
1/2 : x = -2/15
x = 1/2 : (-2/15)
x = -15/4
c) -2/3 : x + 5/8 = -7/12
-2/3 : x = -7/12 - 5/8
-2/3 : x = -33/8
x = -2/3 : (-33/8)
x = 16/99
d) 1/2 x + 2 1/2 = 3 1/2 x - 3/4
1/2 x + 5/2 = 7/2 x - 3/4
7/2 x - 1/2 x = 5/2 + 3/4
3x = 13/4
x = 13/4 : 3
x = 13/12
 giúp e bài 4,5 với
giúp e bài 4,5 với




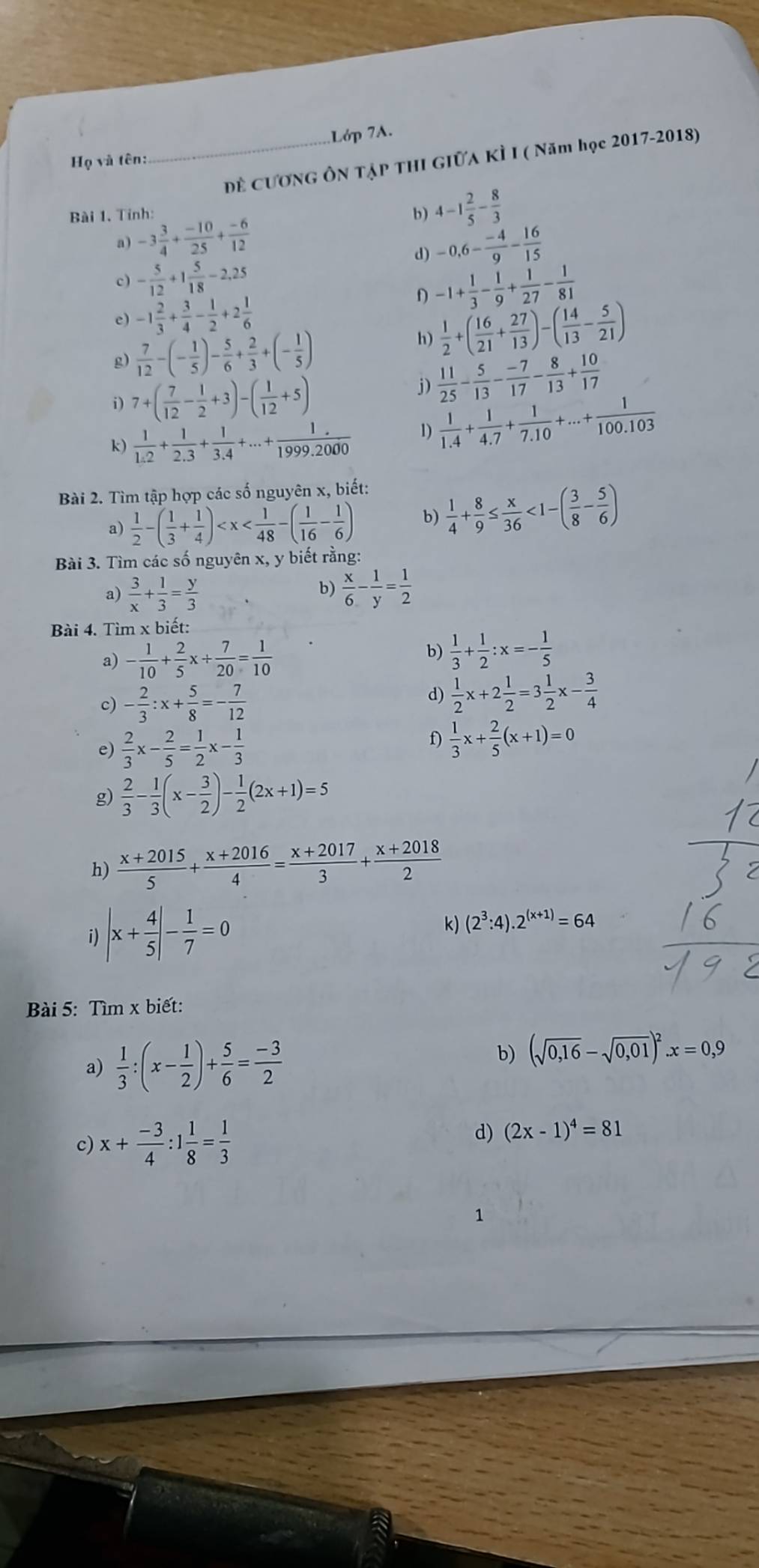

Vì ABCD là hình chữ nhật ( gt )
⇒ ∠DAB = ∠ABC = ∠BCD = ∠CDA = \(90^o\)
Vì AH ⊥ BD ( gt )
⇒ ∠AHD = ∠AHB = \(90^o\)
Xét △ADH và △BDA, có
∠AHD = ∠BAD ( = \(90^o\) )
∠ADB chung
⇒ △ADH ∼ △BDA (g-g)
b) Xét △AHB vuông tại H, có :
∠HAB + ∠ABH = \(90^o\) (Tính chất tam giác vuông)
Mà ∠DAH + ∠HAB = \(90^o\)
⇒ ∠DAH = ∠ABH
Xét △ADH và △BAH, có :
∠DAH = ∠ABH (cmt)
∠AHD = ∠AHB (=\(90^o\))
⇒ △ADH ∼ △BAH (g-g)
⇒ \(\dfrac{AH}{BH}=\dfrac{DH}{AH}\left(TSĐD\right)\)
⇒ \(AH^2=BH.DH\)
c) \(AH^2=DH.BH\left(cmt\right)\)
⇒ \(AH^2=144\)
⇒ AH = 12cm
Xét △ADH vuông tại D, có :
\(AH^2+DH^2=AD^2\) (Định lí Py - ta - go)
\(12^2+9^2=AD^2\)
⇒ \(AD^2=225\)
⇒ AD = 15cm
Vì △ADH ∼ △BAH (cmt)
⇒ \(\dfrac{AD}{AB}=\dfrac{AH}{BH}\)
⇒ \(AB=\dfrac{AD.BH}{AH}\)
⇒ AB = 20cm
d) Xét △AHB, có :
K là trung điểm của AH ( gt )
M là trung điểm của BH ( gt )
⇒KM là đường trung bình của △AHB
⇒KM // AB
\(KM=\dfrac{1}{2}AB\)
Vì ABCD là hình chữ nhật ( gt )
⇒ AB // CD
AB = CD
Có KM // AB (cmt)
AB // CD (cmt)
⇒ KM // CD
Vì N là trung điểm của DC ( gt )
⇒ DN = NC =\(\dfrac{1}{2}CD\)
\(KM=\dfrac{1}{2}AB\) (cmt)
AB = CD (cmt)
⇒ KM = DN = NC
Xét tứ giác KMND, có :
KM = DN (CMT)
KM // DN (CMT)
⇒ KMND là hình bình hành
Vì ABCD là hình chữ nhật ( gt )
⇒ AB ⊥ AD
Mà : KM // AB (cmt)
⇒ KM ⊥ AD
Gọi Q là giao điểm của KM với AD
⇒ QM là đường cao của △AMD
Xét △AMD, có :
QM là đường cao của △AMD (cmt)
AH là đường cao của △AMD (AH⊥BC)
AH cắt QM tại K
⇒ KD là đường cao của △AMD
⇒ KD ⊥ AM
Vì KMND là hình bình hành (cmt)
⇒ KD // MN
KD ⊥ AM (CMT)
⇒ MN ⊥ AM
⇒ ∠AMN = \(90^o\)