Cho các hàm số f1(x)=\(\frac{1}{x}\);f2(x)=x2. Chứng tỏ trong các hàm số trên có tính chất
f(x1.x2)=f(x1).f(x2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 11 2017
Dựa vào đồ thị, suy ra 
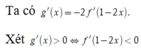
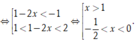
Vậy g(x) đồng biến trên các khoảng 
Chọn D.
CM
30 tháng 8 2019
Đáp án A
Đặt f 1 = a f ' 1 = b , thay x = 0 vào giả thiết, ta được f 2 1 = - f 3 0 ⇔ a 3 + a 2 = 0 ⇔ [ a = 0 a = - 1
Đạo hàm cả 2 vế biểu thức f 2 1 + 2 x = x - f 3 1 - x , ta đưuọc
4 f ' 1 + 2 x . f 1 + 2 x = 1 + 3 f ' 1 - x . f 2 1 - x 1
Thay x = 0 vào (1), ta có 4 f ' 1 . f 1 = 1 + 3 f ' 1 . f 2 1 ⇔ 4 a b = 1 + 3 a 2 b 2
TH1. Với a = 0 thay vào (2), ta được 0 = 1 (vô lí)
TH2. Với a = -1 thay vào (2), ta được - 4 b = 1 + 3 b ⇔ b = - 1 7 ⇒ f ' 1 = - 1 7
Vậy phương trình tiếp tuyến cần tìm là y - f 1 = f ' 1 x - 1 ⇒ y = - 1 7 x - 6 7 .
CM
30 tháng 7 2019
Ta có 
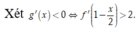
= TH1: 
Do đó hàm số nghịch biến trên (-4;-2)
= TH2: 
nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
Vậy hàm số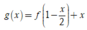 
nghịch biến trên (-4;-2)
Chọn A.
CM
14 tháng 2 2018
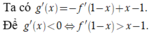
Đặt t = 1 - x, bất phương trình trở thành f'(t) > -t
Kẻ đường thẳng y = -x cắt đồ thị hàm số f'(x) lần lượt tại ba điểm x = -3, x = -1, x = 3 (như hình vẽ)
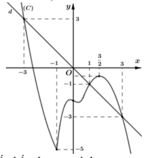
Quan sát đồ thị ta thấy bất phương trình
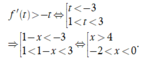
Đối chiếu đáp án ta chọn B.
