cho các số thức x;a;b;c thay đổi thỏa mãn hệ pt \(\int^{x+a+b+c=7\left(1\right)}_{x^2+a^2+b^2+c^2=13\left(2\right)}\)tìm GTNN và GTLN của x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 2 2019
Ta có
(1 - 2i)x + (1 + 2i)y = 1 + i
<=> (x + y) + (2y - 2x)i = 1 + i
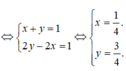
Chọn đáp án A.
CM
21 tháng 7 2018
Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
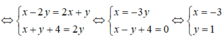
Vậy x = -3, y = 1.
Chọn đáp án D.
L2
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
\(xy+x+1=3y\Rightarrow x+\dfrac{1}{y}+\dfrac{x}{y}=3\)
Ta có:
\(x^3+1+1\ge3x\)
\(\dfrac{1}{y^3}+1+1\ge\dfrac{3}{y}\)
\(x^3+\dfrac{1}{y^3}+1\ge\dfrac{3x}{y}\)
Cộng vế:
\(2\left(x^3+\dfrac{1}{y^3}\right)+5\ge3\left(x+\dfrac{1}{y}+\dfrac{x}{y}\right)=9\)
\(\Rightarrow x^3+\dfrac{1}{y^3}\ge2\)
\(\Rightarrow x^3y^3+1\ge2y^3\) (đpcm)
Dấu "=" xảy ra khi \(x=y=1\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
\(x^3+x\ge2\sqrt{x^4}=2x^2\)
Tương tự:
\(y^3+y\ge2y^2\)
\(z^3+z\ge2z^2\)
Cộng vế:
\(x^3+y^3+z^3+x+y+z\ge2\left(x^2+y^2+z^2\right)=6\)
Dấu "=" xảy ra khi \(x=y=z=1\)
KS
2
CM
26 tháng 5 2018
Ta có: 2 < 5 ⇔ 2 + - x < 5 + - x ∀ x
Hay 2 – x < 5- x
Chọn D.
CM
1 tháng 2 2017
Đáp án C
Ta có 3 x = 5 y = 15 2017 x + y − z = k và 2017 x + y − z = t suy ra 3 = k 1 x 5 = k 1 y và 15 = k 1 t
Khi đó 3.5 = k 1 t ⇔ k 1 x . k 1 y = k 1 t ⇔ k 1 x + 1 y = k 1 t ⇔ t x + y = x y ⇔ 2017 − x + y z = x y
Vậy x y + y z + x z = 2017 → S ∈ 0 ; 2018
NM
0