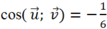Cho các véctơ a → ; b → có độ dài bằng 1 và góc tạo bởi hai vectơ bằng 600. Xác định cosin góc giữa hai vectơ u → = a → + 2 b → ; v → = a → - b →
A. -1/2
B. -1/4
C. -1/6
D. 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Phương trình đường thẳng qua hai điểm A, O có dạng 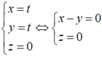
Gọi (P) là mặt phẳng cùng đi qua hai điểm A, O nên (P) : m (x-y)+nz=0, m²+n² > 0. Khi đó véctơ pháp tuyến của (P) có dạng ![]()
![]()
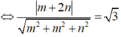
![]()
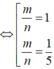
Vậy một véctơ pháp tuyến của một trong hai mặt phẳng đó là 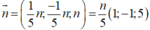

a) Trong mặt phẳng tọa độ Oxy cho vectơ →a =(a1;a2) và vectơ đối của véctơ a là véctơ→b = –→a ⇒ →b = (-a1; -a2). Vật khẳng định hai véctơ đối nhau thì chúng có hoành độ đối nhau là đúng.
b) Trong mặt phẳng tọa độ Oxy véctơ →i =(1;0); Véctơ →a ≠ →0 cùng phương với véctơ→i khi a = k→i với k∈R. Suy ra →a =(k;0) với k≠0. Vậy khẳng định véctơ →a ≠ 0 cùng phương với véctơ →i nếu →a có hoành độ bằng 0 là sai.
c) Trong mặt phẳng tọa độ Oxy véctơ →j = (0;1); véctơ →a cùng phương với véctơ →j khi a = k→j với k∈R. Suy ra →a =(0;k) với k∈R. Vậy khẳng định véctơ →a có hoành độ bằng 0 thì cùng phương với véctơ →j là đúng.
Chọn C.
Ta có:
Mặt khác :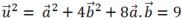 nên
nên 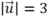
Suy ra