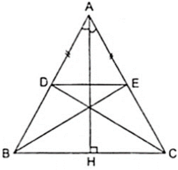
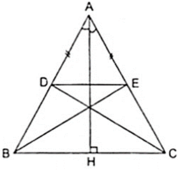
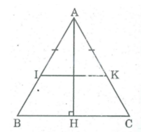
Cho△ABC cân tại A , đường cao AH . Lấy M ∈ cạnh AB ; N ∈ tia đối tia CA sao cho BM = NC . MN cắt BC tại I . Kẻ ND // AB ( D ∈ tia BC )
a) CMR : BMND là hình bình hành
b) Kẻ OI ⊥ MN ( O ∈ tia AH)
CMR : ΔOBM = ΔOCN
c) CMR : OC ⊥ AN
d) CMR : 1/AB2 + 1/OB2 = 4/BC2


c)
Theo phần b: \(\triangle OBM=\triangle OCN\Rightarrow \angle OBM=\angle OCN(1)\)
Ta cũng thấy:
\(AO\) là trung trực của $BC$ (đã chỉ ra ở phần b) nên \(AB=AC, OB=OC\)
Do đó: \(\triangle ABO=\triangle ACO\) (c.c.c)
\(\Rightarrow \angle ABO=\angle ACO\) hay \(\angle OBM=\angle ACO(2)\)
Từ \((1);(2)\Rightarrow \angle ACO=\angle OCN\)
Mà tổng 2 góc trên bằng $180^0$ nên mỗi góc bằng $90^0$
Vậy \(\angle OCN=90^0\Rightarrow OC\perp AN\)
d)
Ta có: \(\angle OBM=\angle OCN=90^0\Rightarrow AB\perp OB\)
Tam giác vuông tại $B$ là $ABO$ có đường cao $BH$ nên theo công thức hệ thức lượng trong tam giác vuông, ta thu được kết quả:
\(\frac{1}{AB^2}+\frac{1}{BO^2}=\frac{1}{1}{BH^2}=\frac{1}{(\frac{BC}{2})^2}=\frac{4}{BC^2}\) (do tam giác $ABC$ cân tại $A$ nên chân đường cao $H$ đồng thời cũng là trung điểm của $BC$)
Ta có đpcm.
Hình vẽ: