Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H K I E
Xét ΔABC cân tại A(gt).Mà AH là đường cao(gt)
=>AH cx là đường phân giác
=>^IAE=^KAE
Xét ΔIAE và ΔKAE có:
AI=AK(gt)
^IAE=^KAE(cmt)
AE:cạnh chung
=>ΔIAE=ΔKAE(c.g.c)
=>IE=KE (1)
Xét ΔAIK có AI=AK(gt)
=> ΔAIK cân tại A
Mà AE là đường pg
=>AE cx là đường cao
=> IK\(\perp\)AH (2)
Từ (1) và (2) suy ra:
I đối xứng với K qua AH

A B C I K H
Ta có: \(\Delta ABC\) cân , AH là đường cao nên AH cũng là phân giác góc A
mà \(\Delta AIK\) cân , AH là tia phân giác nên AH cũng là trung trực của IK
Vậy I đối xứng với K qua AH
Vì tam giác ABC cân tại A, AH là đường cao nên AH là tia phân giác của góc A.
Do tam giác AIK cân tại A, AH là tia phân giác của góc A nên AH là đường trung trực của IK.
Vậy I đối xứng với K qua AH

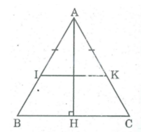
Ta có: △ ABC cân tại A; AH ⊥ BC (gt)
Suy ra: AH là tia phân giác của góc A
Lại có: AI = AK (gt)
Suy ra: ∆ AIK cân tại A
Do AH là tia phân giác của góc A
Nên AH là đường trung trực của IK
Vậy I đối xứng với K qua AH.

A B C H I K
a) Ta có AI = AK ; AB = AC => AI / AB = AK/ AC => IK // BC (Định lí Ta lét)
Tam giác ABC cân tại A có AH là đường cao => AH I BC
=> AH I IK
Mặt khác, tam giác AIK cân tại A : AH là đường cao nên đồng thời là đường trung trực
=> I và K đối xứng qua AH

chỉ là gợi ý thôi
nối i với h và k với c chứng minh tam giác ibh bằng tam giác kch(cgc) suy ra ih=kh\(\Rightarrow\)h thuộc đường trung trực của ik
ai=ak \(\Rightarrow\)a thuộc đường trung trực của ik
DÓ ĐÓ AH là đường trung trực của IK\(\Rightarrow\)I đối xứng với điểm K qua AH

a: Xét ΔEBH và ΔFCH có
EB=FC
\(\widehat{B}=\widehat{C}\)
BH=CH
Do đó: ΔEBH=ΔFCH
Suy ra: HE=HF
hay H nằm trên đường trung trực của EF(1)
Ta có: AE=AF
nên A nằm trên đường trung trực của EF(2)
Từ (1) và (2) suy ra E và F đối xứng nhau qua AH


A B C I K H O
Gọi giao điểm của IK và AH là O.
Vì ΔABC cân tại A và AH là đường cao
=> AH đồng thời cũng là tia phân giác của ΔABC
hay AO là tia phân giác của \(\widehat{IAK}\)
=> \(\widehat{IAO}=\widehat{OAK}\)
Xét ΔAIO và ΔAKO có: \(\left\{{}\begin{matrix}AI=AK\left(gt\right)\\\widehat{IAO}=\widehat{KAO}\\AO chung\end{matrix}\right.\)
=> ΔAIO = ΔAKO(c.g.c)
=>IO=KO(2 cạnh tương ứng)
Xét ΔAIK cân tại A (AI=AK) có AO là đường trung tuyến
=> AO là đương trung trực của \(\Delta\) AIK
=> I đối xứng với K qua AH
=>đpcm
Ta có: AI+IB=AB(I nằm giữa A và B)
AK+KC=AC(K nằm giữa A và C)
mà AI=AK(gt)
và AB=AC(ΔABC cân tại A)
nên IB=KC
Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(Hai cạnh tương ứng)
Xét ΔIBH và ΔKCH có
IB=KC(cmt)
\(\widehat{B}=\widehat{C}\)(ΔBAC cân tại A)
BH=CH(cmt)
Do đó: ΔIBH=ΔKCH(c-g-c)
Suy ra: HI=HK(Hai cạnh tương ứng)
Ta có: AI=AK(gt)
nên A nằm trên đường trung trực của IK(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: HI=HK(cmt)
nên H nằm trên đường trung trực của IK(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AH là đường trung trực của IK
hay I đối xứng với K qua AH(đpcm)