Cho hình bình hành ABCD .Gọi I là giao điểm của hai đường chéo AC và BD;M,N theo thứ tự là trung điểm của ID và IB
a,Chứng minh rằng AM//CN
b,Kéo dài AM cắt DC tại E chứng minh DE =1/2 EC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 11 2021
Đáp án: Giải thích các bước giải a) Hình bình hành ABCD gọi OO là giao điểm của AC và BD ⇒O⇒O là trung điểm của AC, BD (tính chất ) Xét hai tam giác vuông ΔOEBΔOEB và OFDOFD có: OB=ODOB=OD ˆBOE=ˆDOFBOE^=DOF^ (đối đỉnh) ⇒ΔOEB=ΔOFD⇒ΔOEB=ΔOFD (cạnh huyền-góc nhọn) ⇒BE=DF⇒BE=DF (hai cạnh tương ứng) Và có BE//DFBE//DF (vì cùng vuông góc với AC giả thiết) Từ hai điều trên ⇒⇒ tứ giác BEDF là hình bình hành (dấu hiệu nhận biết) b) Xét ΔHBCΔHBC và ΔKDCΔKDC có: ˆBHC=ˆDKC=90oBHC^=DKC^=90o (giả thiết) ˆHBC=ˆKDCHBC^=KDC^ (=ˆBAD=BAD^ đồng vị) ⇒ΔHBC∼ΔKDC⇒ΔHBC∼ΔKDC (g.g) ⇒CHCK=CBCD⇒CHCK=CBCD (hai cạnh tương ứng tỉ lệ) ⇒CH.CD=CK.CB⇒CH.CD=CK.CB (đpcm) c) Xét ΔAEBΔAEB và ΔAHCΔAHC có: ˆAA^ chung ˆAEB=ˆAHC=90oAEB^=AHC^=90o ⇒ΔAEB∼ΔAHC⇒ΔAEB∼ΔAHC (g.g) ⇒AEAH=ABAC⇒AEAH=ABAC (hai cạnh tương ứng tỉ lệ) ⇒AE.AC=AB.AH⇒AE.AC=AB.AH (1) Xét ΔAFDΔAFD và ΔAKCΔAKC có: ˆAA^ chung ˆAFD=ˆAKC=90oAFD^=AKC^=90o ⇒ΔAFD=ΔAKC⇒ΔAFD=ΔAKC (g.g) ⇒AFAK=ADAC⇒AFAK=ADAC (hai cạnh tương ứng bằng nhau) ⇒AF.AC=AK.AD⇒AF.AC=AK.AD (2) Ta có OE=OF (suy ra từ ΔOEB=ΔOFDΔOEB=ΔOFD câu a) OA=OC (tính chất hình bình hành) ⇒OA−OE=OC−OF⇒OA−OE=OC−OF hay AE=FCAE=FC (3) Từ (1), (2) và (3) suy ra AB.AH+AK.AD=AE.AC+AF.ACAB.AH+AK.AD=AE.AC+AF.AC =AC(AE+AF)=AC(FC+AF)=AC2=AC(AE+AF)=AC(FC+AF)=AC2 (đpcm)
CH
15 tháng 10 2023
Chứng minh k,o, i thẳng hàng:
ABCD là HBH
=> BC và AC cắt nhau tại trung điểm của mỗi đường
Mà: O là giao điểm của CB và AC
=> O là trung điểm của AC
Tứ giác AKCI có: AK = IC (GT); AK // IC (ABCD là HBH)
=> AKCI là HCH
=> AC và IK cắt nhau tại trung điểm của mỗi đường
Mà: O là trung điểm của AC
=> O là trung điểm của IK
=> O,I,K thẳng hàng
M
29 tháng 12 2022
\(3\overrightarrow{AP}-2\overrightarrow{AC}=\overrightarrow{0}\)
\(VT=3\left(\overrightarrow{AD}+\overrightarrow{DP}\right)-2\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\)
\(=3\overrightarrow{AD}+3\overrightarrow{DP}-2\overrightarrow{AD}-2\overrightarrow{DC}\)
\(=\overrightarrow{AD}+3\overrightarrow{DP}-2\overrightarrow{DC}\)
\(=\overrightarrow{AD}+3\left(\overrightarrow{DC}+\overrightarrow{CP}\right)-2\overrightarrow{DC}\)
\(=\overrightarrow{AD}+3\overrightarrow{DC}+3\overrightarrow{CP}-2\overrightarrow{DC}\)
\(=\widehat{AD}+\overrightarrow{DC}+3.\dfrac{2}{3}\overrightarrow{CO}\)
\(=\overrightarrow{AD}+\overrightarrow{DC}+2.\dfrac{1}{2}\overrightarrow{CA}\)
\(=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CA}\)
\(=\overrightarrow{AC}+\overrightarrow{CA}\)
\(=\overrightarrow{AA}=\overrightarrow{0}=VP\) (điều phải chứng minh)
1 tháng 9 2023
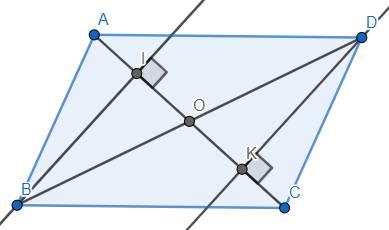
b) Vì BI vuông góc với AC tại I, nên I thuộc AC.
Vì DK vuông góc với AC tại K, nên K thuộc AC.
Vì O là giao điểm của AC và BD nên O thuộc AC.
Suy ra I, O, K là các điểm thuộc AC; từ đó ba điểm I, O, K thẳng hàng
CM
20 tháng 5 2017
Theo tính chất hình bình hành ta có: I là trung điểm của AC và BD.
Suy ra:
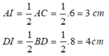
Xét tam giác AID có: A I 2 + I D 2 = A D 2 ( 3 2 + 4 2 = 5 2 = 25 )
Suy ra: tam giác AID là tam giác vuông: AI ⊥ DI hay AC ⊥ BD
Hình bình hành ABCD có 2 đường chéo AC và BD vuông góc với nhau nên là hình thoi.
Suy ra: AB = BC = CD = DA = 5cm
Chọn đáp án B
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
IA = IC và IB = ID => Điểm I là trung điểm của hai đường chéo AC và BD.
a: Ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường
mà I là giao điểm của AC và BD
nên I là trung điểm chung của AC và BD
Suy ra: IB=ID
mà \(IM=\dfrac{ID}{2}\)
và \(IN=\dfrac{IB}{2}\)
nên IM=IN
Xét tứ giác AMCN có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo MN
Do đó: AMCN là hình bình hành
Suy ra: AM//CN