trên tia Ax lấy 2 điểm E;F sao cho : AE=3,5 , AF=7
a) trong 3 điểm A:Ế:F điểm nào nằm giữa
b) tinh EF
c) điểm E có là trung điểm đoạn thẳng AF không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

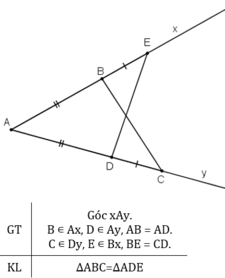
Ta có: AB = AD, BE = DC ⇒ AB + BE = AD + DC hay AE = AC.
Xét ΔABC và Δ ADE có:
AC = AE (cmt)
Góc A chung
AB = AD (gt)
⇒ ΔABC = ΔADE (c.g.c)

FD//EG
Áp dụng định lý Ta let ta có:
\(\frac{AD}{AE}=\frac{AF}{AG}\) (1)
FE // GH
Áp dụng định lý Ta lét ta có:
\(\frac{AE}{AH}=\frac{AF}{AG}\) (2)
Từ (1) và (2) => \(\frac{AD}{AE}=\frac{AE}{AH}\)
=> AE²=AD.AH (đpcm)
Nguồn: nttxyhthkbgd1

Vì Ax//By;C,E thuộc Ax;D,F thuộc By=>Ac//BD, AE//BF
=>góc CAO=góc OBD
Góc AEO=góc OFD
Góc ACO= góc ODB
xét tam giác ACO và tam giác OBD ta có
OA=OB;Góc CAO=BOD;ACO=ODB
=>hai tam giác này bằng nhau
=>góc COA=BOD(2 góc tương ứng )
Mà A,O,B thửng hàng=>góc COB+COA=180 độ
=>góc BOD+COB=180 độ
=>O,C,D thẳng hàng
tương tự chứng minh với E,O,F
b,Từ những tam giác bằng nhau ta có được OE=OF;CO=OD
xét tam giác OED và OCF có OE=OF; CO=OD; góc COF=EOD( 2 góc đối đỉnh)
=>góc FOD=CDE; DE=CF(2 cạnh tương ứng)
mà hai góc này ở vị trí so le trong của hai đoạn thẳng DE và CF được cắt bởi đoạn DC
=>DE//CF
má ơi trình bày trên máy tính khó qua cơ. gấp 3 lần thời gian trình bày ở vở luôn
ý:(((
(

Bài 4:
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
BA chung
AC=AD
Do đó: ΔABC=ΔABD
b: Xét ΔMAC vuông tại A và ΔMAD vuông tại A có
MA chung
AC=AD
Do đó: ΔMAC=ΔMAD
Xét ΔMBD và ΔMBC có
MB chung
BD=BC
MD=MC
Do đó: ΔMBD=ΔMBC
a) Vì AE < AF (3,5cm < 7cm)
nên E nằm giữa A và F
b) Vì E nằm giữa nên ta có:
AE + EF = AF
3,5 + EF = 7
EF = 7 - 3,5
EF = 3,5cm
c) Vì AE = EF (3,5cm = 3,5cm)
nên \(AE=EF=\frac{AF}{2}=\frac{7}{2}=3,5cm\)
Vậy E là trung điểm của AF
thêm đơn vị là cm nữa nhé bạn .
a) Trong ba điểm ta gọi là : AEF
=> AEF . Nên E nằm giữa 2 điểm AF
b) Vì EA = 3,5 cm
AF = 7 cm
Nên EF= 7-3,5 = 3,5 cm
c) Dựa vào bài b .
vì : EA = EF = \(\frac{AF}{2}\)=\(\frac{7}{2}\)=\(3,5\)cm
=> E là trung điểm của AF