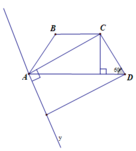
Cho hình thanh cân ABCD, AD//BC có AB = BC = CD = a; AD = 2a. Thể tích của khối tròn xoay thu được khi xoay hình thang theo trục AC là
A. πa 2 3 3 .
B. πa 3 3 3 .
C. πa 6 3 3 .
D. πa 3 3 9 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn hệ trục Oxy trong đó A = O, Ox = AC. Hình thang thỏa mãn bài toán có A C ⊥ C D , góc đáy bằng 60 O , A C = A D . sin 60 o = a 3 ⇒ D a 3 ; a . PT đường thẳng AD là y = 1 3 x
Vậy thể tích cần tính
V = π ∫ 0 a 3 1 3 x 2 dx = π 9 x 3 0 a 3 = πa 3 3 3
Đáp án cần chọn là B

Hạ CH và DK vuông góc với AB
Ta có:
A K = B H = 1 2 A D = 1 c m
Từ đó: CD = 2,5cm
C H = 3 c m
S A B C D = A B + C D . C D 2 = 7 3 2 c m 2


Qua P kẻ đường thẳng song song với AD cắt CD tại P. Khi đó dễ thấy \(AB=DP\). Từ đó \(DC-AB=DC-DM=CM\)
Mặt khác, \(AD=BM\) nên \(AD+BC=BM+BC\).
Hiển nhiên \(CM< BM+BC\). Điều này dẫn đến \(DC-AB< AD+BC\) (đpcm)

từ A hạ \(AE\perp DC\)
từ B hạ \(BF\perp DC\)
\(AB//CD=>AB//EF\)\(=>ABCD\) là hình chữ nhật
\(=>AB=EF=2cm\)
vì ABCD là hình thang cân\(=>\left\{{}\begin{matrix}AD=BC\\\angle\left(ADE\right)=\angle\left(BCF\right)\end{matrix}\right.\)
mà \(\angle\left(AED\right)=\angle\left(BFC\right)=90^o\)
\(=>\Delta ADE=\Delta BFC\left(ch.cgn\right)=>DE=FC=\dfrac{DC-EF}{2}=\dfrac{6-2}{2}=2cm\)
xét \(\Delta ADE\) vuông tại E có: \(AE=\sqrt{AD^2-ED^2}=\sqrt{3^2-2^2}=\sqrt{5}cm\)
\(=>S\left(ABCD\right)=\dfrac{\left(AB+CD\right)AE}{2}=\dfrac{\left(2+6\right)\sqrt{5}}{2}=4\sqrt{5}cm^2\)

A B C B
Đề bài phải sửa thành "biết AD=AB" mới làm được
a/
ABCD là hình thàng cân => AD=BC
Mà AD=AB (gt)
=> AD=BC
b/
ABCD là hình thang cân
\(\Rightarrow\widehat{BAD}=\widehat{ABC}\)
\(\widehat{BCD}+\widehat{ABC}=180^o\) (Hai góc trong cùng phía)
\(\Rightarrow\widehat{BCD}+\widehat{BAD}=180^o\)
=> ABCD là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bù nhau là tứ giác nt)
Ta có
Cung AB và cung BC có hai dây trương cung bằng nhau
AB=BC (cmt) => sđ cung AB = sđ cung BC (1)
\(sđ\widehat{ADB}=\dfrac{1}{2}sđcungAB\) (góc nội tiếp) (2)
\(sđ\widehat{CDB}=\dfrac{1}{2}sđcungBC\) (góc nội tiếp) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{ADB}=\widehat{CDB}\) => DB là phân giác của \(\widehat{ADC}\)

Kéo dài AD và BC, chúng cắt nhau tại M, dựng đường cao DH.
⇒ tam giác ABM đều.⇒AB=AM=4,5⇒DC=AM-AD=4,5-2=2,5Xét tam giác ADH vuông tại D có ADH=30AH=1/2AD=1/2.2=1Mặt khác ta có:DH²=AD²-AH²(theo định lý PITAGO)⇒DH²=4-1=3⇒DH=√3⇒Sabcd=(DC+AB).DH/2=(2,5+4,5).√3/2=7√3/2
Đáp án B
Chọn hệ trục Oxy trong đó A ≡ O ; O x ≡ A C
Hình thang thỏa mãn bài toán có A C ⊥ C D , góc đáy bằng 60 o
⇒ PT đường thẳng AD là y = 1 3 x
Vậy thể tích cần tính