: Cho hình thang ABCD( AB //CD).
Biết AB = 3cm; AD = 2,5cm;BD = 6cm và DBC = DAB .
a. Chứng minh hai tam giác ADB và BCD đồng dạng.
b. Tính độ dài các cạnh BC và CD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

từ A hạ \(AE\perp DC\)
từ B hạ \(BF\perp DC\)
\(AB//CD=>AB//EF\)\(=>ABCD\) là hình chữ nhật
\(=>AB=EF=2cm\)
vì ABCD là hình thang cân\(=>\left\{{}\begin{matrix}AD=BC\\\angle\left(ADE\right)=\angle\left(BCF\right)\end{matrix}\right.\)
mà \(\angle\left(AED\right)=\angle\left(BFC\right)=90^o\)
\(=>\Delta ADE=\Delta BFC\left(ch.cgn\right)=>DE=FC=\dfrac{DC-EF}{2}=\dfrac{6-2}{2}=2cm\)
xét \(\Delta ADE\) vuông tại E có: \(AE=\sqrt{AD^2-ED^2}=\sqrt{3^2-2^2}=\sqrt{5}cm\)
\(=>S\left(ABCD\right)=\dfrac{\left(AB+CD\right)AE}{2}=\dfrac{\left(2+6\right)\sqrt{5}}{2}=4\sqrt{5}cm^2\)

Kẻ BH//AD(H∈CD)BH//AD(H∈CD), kẻ BD
Ta có:
+) AB//CD (hình thang ABCD)
⇒B2ˆ=D1ˆ⇒B2^=D1^ ( 2 góc so le trong )
+) BH//AD (cách vẽ)
⇒D2ˆ=B1ˆ⇒D2^=B1^ ( 2 góc so le trong)
Xét ΔDABΔDAB và ΔBHDΔBHD, ta có:
B2ˆ=D1ˆ(cmt)B2^=D1^(cmt)
BD : chung
D2ˆ=B1ˆ(cmt)D2^=B1^(cmt)
⇒⇒ ΔDABΔDAB = ΔBHDΔBHD (gcg)
⇒AD=BH⇒AD=BH
mà AD=3cm(gt)AD=3cm(gt)
⇒BH=3cm⇒BH=3cm
+) ΔDABΔDAB = ΔBHDΔBHD (cmt)
⇒AB=DH⇒AB=DH
mà AB=4cm(gt)AB=4cm(gt)
⇒DH=4cm⇒DH=4cm
+) DH+HC=DC(H∈DC)DH+HC=DC(H∈DC)
⇒4+HC=8⇒4+HC=8
⇒HC=4cm⇒HC=4cm
Xét ΔBHC,ΔBHC, ta có:
52=32+4252=32+42
⇒BC2=BH2+HC2⇒BC2=BH2+HC2 (Định lý Py-ta-go)
⇒ΔBHC⇒ΔBHC vuông tại H
⇒H1ˆ=900⇒H1^=900
+) AD//BH
⇒ADHˆ=H1ˆ⇒ADH^=H1^ (2 góc động vị)
⇒ADHˆ=900⇒ADH^=900
⇒⇒ Hình thang ABCD là hình thang vuông

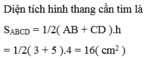
a: Xét ΔADB và ΔBCD có
\(\widehat{BAD}=\widehat{DBC}\)
\(\widehat{ABD}=\widehat{BDC}\)
Do đó: ΔADB\(\sim\)ΔBCD
b: ta có:ΔADB\(\sim\)ΔBCD
nên AD/BC=AB/BD
=>2,5/BC=1/2
hay BC=5(cm)