Cho tam giác ABC, biết AB = 21 ; AC = 28 ; BC = 35
a) Chứng minh rằng tam giác ABC vuông
b) Tính sinB, sinC, góc B, góc C và đường cao AH vủa tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo giả thiết AB : AC = 3 : 4
Suy ra A B 3 = A C 4 = A B + A C 3 + 4 = 3 . Do đó AB = 3.3 = 9 (cm); AC = 3.4 = 12 (cm)
Tam giác ABC vuông tại A, theo định lý Pytago ta có:
B C 2 = A B 2 + A C 2 = 9 2 + 12 2 = 225 , suy ra BC = 15cm
Đáp án cần chọn là: B

\(\dfrac{AB}{AC}=\dfrac{20}{21}\Rightarrow AB=\dfrac{20AC}{21}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{841}{400AC^2}\)
\(\Rightarrow AC=609\) \(\Rightarrow AB=\dfrac{20}{21}AC=580\)
\(BC=\sqrt{AB^2+AC^2}=841\)
Chu vị: \(609+580+841=2030\)

Tam giac ABC đồng dạng tam giác HAC (cùng vuông và có chung góc C)
AB/AC = AH/HC = 20/21
HC = 21AH/20 = 441
==> AC = căn(AH^2 + HC^2) =căn(420^2 + 441^2) = 609
AB/AC = 20/21
AB = 20/21*609 = 580
BC = căn(AB^2 + AC^2) = căn(580^2 + 609^2) = 841
Chu vi tam giác ABC = tổng 3 cạnh
C = AB + AC + BC = 580 + 609 + 841 = 2030

a:
BC=35cm
\(AH=\dfrac{AB\cdot AC}{BC}=16.8\left(cm\right)\)
b: \(AE=\dfrac{AH^2}{AC}=\dfrac{16.8^2}{28}=10.08\left(cm\right)\)
\(AD=\dfrac{AH^2}{AB}=\dfrac{16.8^2}{21}=13.44\left(cm\right)\)
Do đó: \(S_{AED}=\dfrac{AD\cdot AE}{2}=\dfrac{13.44\cdot10.08}{2}=67.7376\left(cm^2\right)\)

A B D ^ = 25 0 . Áp dụng tỉ số lượng giác trong tam giác vuông ABD ta có: BD = 21 cos 25 0 ≈ 21 , 19 c m

Bài làm
Ta có hình vẽ : A B C M Q H 6cm 3cm
a ) Tam giác AMB và AMC có đáy MC = MB và có chung chiều cao hạ từ A xuống MC nên SAMC = SAMB
Mà diện tích của tam giác AMC là : ( MQ + AC ) : 2 = 6 x AC : 2 = 3 x AC
Mà diện tích của tam giác AMB là : ( MC x AB ) : 2 = 3 x AB : 2 = 1,5 x AB
Vì SAMC = SAMB nên 3 x AC = 1,5 x AB = > 2 x AC = AB
b ) Đáy BC dài là : 21 : ( 2 + 1 ) x 2 = 14 ( cm )
Diện tích tam giác AMB là : ( 14 x 3 ) : 2 x 2 = 42 ( cm2 )
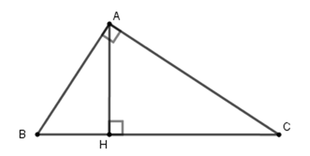
A B C H
Câu a :
Ta có :
\(21^2+28^2=35^2\) ( py - ta - go )
\(\Rightarrow ABC\) vuông tại A .
Câu b :
\(sinB=\dfrac{AC}{BC}=\dfrac{28}{35}=\dfrac{4}{5}=0^048^'0^"\)
\(\sin C=\dfrac{AB}{BC}=\dfrac{25}{35}=\dfrac{5}{7}=0^042^'51,43^"\)