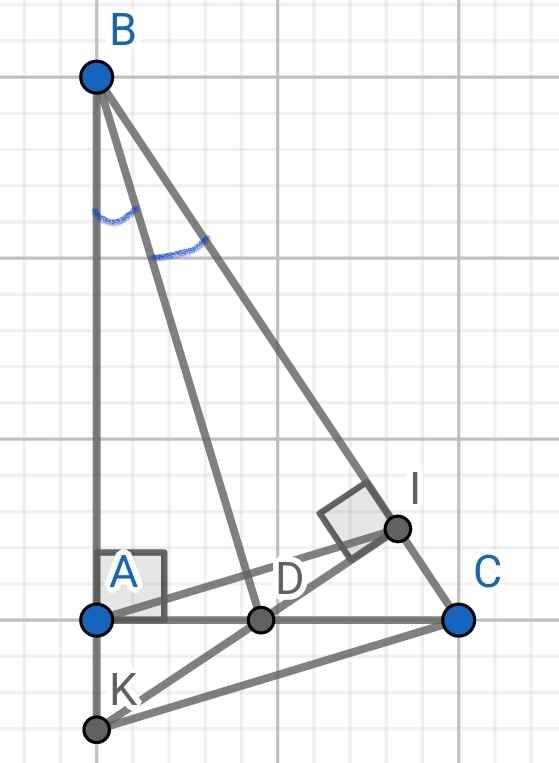
Cho ▲ABC ⊥ A. BD là tia phân giác góc B. Vẽ DI ⊥ BC, (điểm I thuộc BC. Gọi K là giao điểm hai đường thẳng DI và AB
a) Chứng minh: ▲ABD=▲IBD
b) Chứng minh: BD⊥AI
c) Chứng minh: DK=DC
d) Cho AB=6cm; AC=8cm. Hãy tính IC=?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LK
1 tháng 3 2018
a)Xét \(\Delta ABD=\Delta IBD\left(ch-gn\right)\Rightarrow AB=BI;AD=DI.\)
b)Xét \(\Delta ABH=\Delta IBH\left(c-g-c\right)\Rightarrow AHB=IHB=90^0\)
Suy ra \(AI\perp BD\)
c)XÉT \(\Delta ADK=\Delta IDC\left(cgv-gnk\right)\Rightarrow KB=DC\)
d) vì \(BD//EI\Rightarrow DBI=BIE;DBI=BEI\)
HAY \(BIE=BEI\Rightarrow\Delta BIE\)CÂN TẠI B
KV
15 tháng 3 2023
a) Xét hai tam giác vuông: ∆ABD và ∆IBD có:
BD chung
∠ABD = ∠IBD (gt)
⇒ ∆ABD = ∆IBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆IBD (cmt)
⇒ AD = ID (hai cạnh tương ứng)
∆DIC vuông tại I
⇒ DC là cạnh huyền
⇒ ID < DC
Mà AD = ID (cmt)
⇒ AD < DC
c) Xét hai tam giác vuông: ∆DAK và ∆DIC có:
AD = ID (cmt)
∠ADK = ∠IDC (đối đỉnh)
⇒ ∆DAK = ∆DIC (cạnh góc vuông - góc nhọn kề)
⇒ DK = DC (hai cạnh tương ứng)
d) Do ∆DAK = ∆DIC (cmt)
⇒ AK = IC (hai cạnh tương ứng)
Do ∆ABD = ∆IBD (cmt)
⇒ AB = IB (hai cạnh tương ứng)
∆ABI cân tại B
⇒ ∠BAI = ∠BIA = (180⁰ - ∠ABC)/2 (1)
Do AB = IB (cmt)
AK = IC (cmt)
⇒ BK = BC
⇒ ∆BCK cân tại B
⇒ ∠BKC = ∠BCK = (180⁰ - ∠ABC)/2 (2)
Từ (1) và (2) ⇒ ∠BAI = ∠BKC
Mà ∠BAI và ∠BKC là hai góc đồng vị
⇒ AI // KC
BY
13 tháng 2 2018
a) Dễ rồi nhé, trường hợp cạnh huyền góc nhọn
b) 2 tam giác trên bằng nhau (c/m câu a)
=> BA=BI và DA = DI
=> BD là đường trung trực đoạn AI
=> BD _|_ AI
c) Cũng là trường hợp cạnh huyền góc nhọn luôn, do:
DA = DI (c/m câu b); KDA^ = CDI^ (đối đỉnh)
=> bằng nhau thôi
d) AB = 6cm => BI = 6 cm
tính BC bằng đl py-ta-go áp dụng vào tam giác vuông ABC
IC = BC - BI
(xong! Em tự trình bày, có chỗ nào thắc mắc cứ hỏi nhé!)
13 tháng 2 2018
càng ngày càng thấy nản môn hình... :v ...
a) Xét ΔABD và ΔIBD có:
\(\widehat{BAD}=\widehat{BID}=90^o\)
\(\widehat{ABD}=\widehat{IBD}\) ( BD là tia phân giác góc B )
AD chung
=> ΔABD = ΔIBD ( c.h-g.n )
câu b làm sau đc không ?
c) Do ΔABD = ΔIBD ( c/m a )
=> DA = DI ( 2 cạnh tương ứng )
Xét ΔADK và ΔIDC có :
\(\widehat{KAD}=\widehat{CID}=90^o\)
DA = DI ( cmt )
\(\widehat{ADK}=\widehat{IDC}\) ( 2 góc đối đỉnh )
=> ΔADK = ΔIDC ( g.c.g )
=> DK = DC ( 2 cạnh tương ứng )
d) Do ΔABC vuông ở A , áp dụng định lí Pi-ta-go ta có :
BC2 = AB2 + AC2
BC2 = 62 + 82
BC2 = 36 + 64
=> BC2 = 100
\(\Rightarrow BC=\sqrt{100}=10\left(cm\right)\)
Ta có :
\(IC=BC-BI\) (*)
Mặt khác :
AB = BI ( 2 cạnh tương ứng của ΔABD = ΔIBD ) (**)
Từ (*) và (**) ,ta suy ra được :
\(IC=BC-AB\\ IC=10^{cm}-6^{cm}\\ \Rightarrow IC=4\left(cm\right)\)
26 tháng 6 2023
a: Sửa đề: AB=6cm
BC=căn 6^2+8^2=10cm
b: Xét ΔABD vuông tại A và ΔIBD vuông tại I có
BD chung
góc ABD=góc IBD
=>ΔBAD=ΔBID
c: ΔBAD=ΔBID
=>BA=BI
=>ΔBAI cân tại B
d: BA=BI
DA=DI
=>BD là trung trực của AI
f: AD=DI
DI<DC
=>AD<DC
g: Xét ΔBIK vuông tại I và ΔBAC vuông tại A có
BI=BA
góc IBK chung
=>ΔBIK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B
21 tháng 12 2021
a: Xét ΔABD và ΔIBD có
BA=BI
\(\widehat{ABD}=\widehat{IBD}\)
BD chung
Do đó: ΔABD=ΔIBD