Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
b: DA=DM
=>góc DAM=góc DMA

Có gì khong hiểu hỏi lại cj nhé:
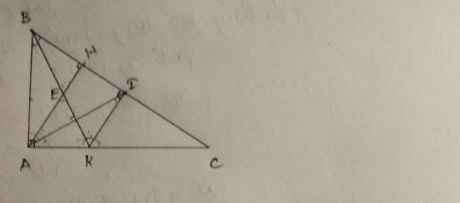
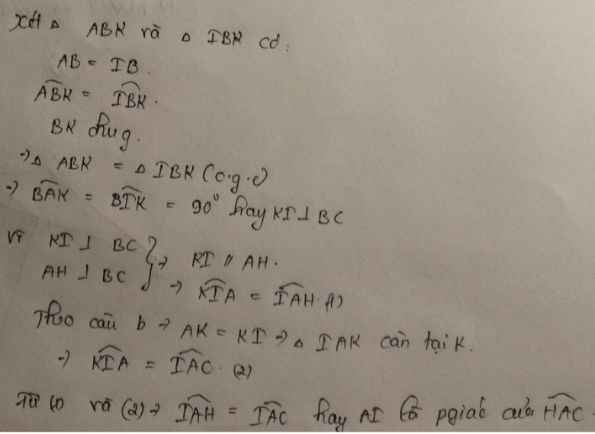
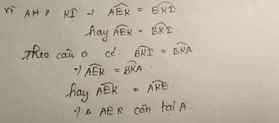
a, b ,c lần lượt từ trên xuống.

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do dó: ΔBAD=ΔBED
=>DA=DE
b: Sửa đề: BD vuông góc với AE
Ta có: BA=BE
DA=DE
Do đó; BD là trung trực của AE
=>BD vuông góc với AE
c: Xét ΔBFC có BA/AF=BE/EC
nên AE//CF

a: \(\widehat{ABD}=\widehat{EBD}=\dfrac{\widehat{EBA}}{2}\)(vì BD là tia phân giác của góc EBA)
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
hay D nằm trên đường trung trực của AE(1)
Ta có: BA=BE
nên B nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD⊥AE
c: Xét ΔCED vuông tại E và ΔKAD vuông tại A có
ED=AD
CE=KA
Do đó: ΔCED=ΔKAD
Suy ra: \(\widehat{CDE}=\widehat{KDA}\)
mà \(\widehat{CDE}+\widehat{EDA}=180^0\)
nên \(\widehat{EDA}+\widehat{KDA}=180^0\)
=>E,D,K thẳng hàng

a: Xét ΔBAI và ΔBKI có
BA=BK
\(\widehat{ABI}=\widehat{KBI}\)
BI chung
Do đó: ΔBAI=ΔBKI
Suy ra: AI=KI

a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD
b: Xét ΔADK vuông tại A và ΔHDC vuông tại H có
DA=DH
\(\widehat{ADK}=\widehat{HDC}\)
Do đó: ΔADK=ΔHDC
Suy ra: DK=DC
a: Xét ΔABD và ΔIBD có
BA=BI
\(\widehat{ABD}=\widehat{IBD}\)
BD chung
Do đó: ΔABD=ΔIBD