Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABK và ΔIBK có
BA=BI
\(\widehat{ABK}=\widehat{IBK}\)
BK chung
Do đó: ΔABK=ΔIBK
Suy ra: \(\widehat{BAK}=\widehat{BIK}=90^0\)
hay KI⊥BC
b: Ta có: \(\widehat{HAI}+\widehat{BIA}=90^0\)
\(\widehat{CAI}+\widehat{BAI}=90^0\)
mà \(\widehat{BIA}=\widehat{BAI}\)
nên \(\widehat{HAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc HAC

b) Ta có: KI\(\perp\)BC(gt)
AH\(\perp\)BC(gt)
Do đó: KI//AH(Định lí 1 từ vuông góc tới song song)
Suy ra: \(\widehat{HAI}=\widehat{KIA}\)(hai góc so le trong)(1)
Ta có: ΔABK=ΔIBK(cmt)
nên KA=KI(hai cạnh tương ứng)
Xét ΔKAI có KA=KI(cmt)
nên ΔKAI cân tại K(Định nghĩa tam giác cân)
Suy ra: \(\widehat{KAI}=\widehat{KIA}\)(hai góc ở đáy)(2)
Từ (1) và (2) suy ra \(\widehat{HAI}=\widehat{KAI}\)
\(\Leftrightarrow\widehat{HAI}=\widehat{CAI}\)
Suy ra: AI là tia phân giác của \(\widehat{HAC}\)(Đpcm)
a) Xét ΔABK vuông tại A và ΔIBK vuông tại I có
BK chung
\(\widehat{ABK}=\widehat{IBK}\)(BK là tia phân giác của \(\widehat{ABI}\))
Do đó: ΔABK=ΔIBK(Cạnh huyền-góc nhọn)

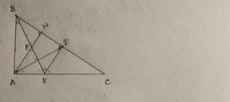
Bạn tự vẽ hình.
a, Sử dụng định lí pitago tính được \(BC=5cm\)
b, Dễ dàng chứng minh \(\Delta ABK=\Delta IBK\left(c.g.c\right)\)
=> \(\widehat{BIK}=\widehat{BAK}=90^o\)
=> \(KI\perp BC\)
c, Ta có: \(\hept{\begin{cases}AH\perp BC\\KI\perp BC\end{cases}}\)
=> AH // KI
=> \(\widehat{HAI}=\widehat{KIA}\) (1)
Mà AK = KI (do \(\Delta ABK=\Delta IBK\))
=> \(\Delta AKI\) cân tại K
=> \(\widehat{KAI}=\widehat{KIA}\) (2)
Từ (1) và (2) => \(\widehat{HAI}=\widehat{KAI}\)
=> AI là tia phân giác \(\widehat{HAC}\)
d, \(\Delta AEK\) có AI là phân giác => \(\Delta AEK\) cân tại A

a, xét tam giác ABM và tam giác KBM có: AB=BK, BM chung, góc ABM= góc KBM
suy ra 2 tam giác trên bằng nhau
hok tốt
tu ve hinh :
xet tamgiac ABM va tamgiac KBM co : MB chung
goc ABM = goc MBK do BM la phan giac cua goc ABC (gt)
AB = AK (gt)
=> tammgiac ABM = tamgiac KBM (c - g - c)

a) Xét \(\Delta BAI\)và \(\Delta BAC\)có :
AB : cạnh chung
\(\widehat{BAI}=\widehat{BAC}\left(=90^0\right)\)
AC = AI ( gt )
\(\Rightarrow\Delta BAI=\Delta BAC\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABI}=\widehat{ABC}\)( do 2 tam giác = nhau )
Mà \(\widehat{ABI}+\widehat{BAH}=90^0\)( tổng 3 góc = 1800 mà có 1 góc = 900 ( do AH\(\perp\)BI ) nên tổng 2 góc còn lại = 900 )
\(\Rightarrow\widehat{ABC}+\widehat{BAK}=90^0\)
\(\Rightarrow\widehat{BAH}=\widehat{BAK}\)
=> BA là đường phân giác của \(\widehat{HBK}\)
b) Ta có tam giác vuông ABK = CBA ( ch-gn ) => AB2 = BK . BC (1)
Ta có tam giác vuông ABH = IBA ( ch-gn ) => AB2 = BH . BI (2)
Từ (1) và (2) => BK . BC = BH . BI => HK // IC ( theo định lí Ta-let )
c) Gọi E là giao điểm của HK và BA
Có tam giác BHK cân ( BE là đường cao, phân giác ) => BH = BK
Ta có BA là đường trung trực của HK => HA = KA
Có tam giác vuông BHN = BKM ( gn-cgv ) => HN = KM
=> HA + AN = AK + AM => AN = AM => Tam giác AMN cân tại A
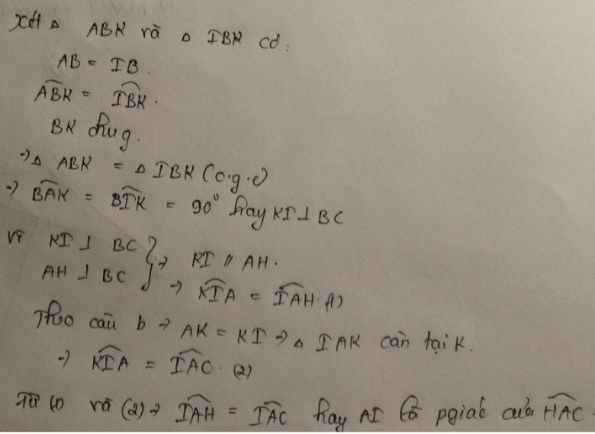
Có gì khong hiểu hỏi lại cj nhé:
a, b ,c lần lượt từ trên xuống.
Chị tâm lí qué=)