Cho hình chóp S.ABCD có đáy ABCD là hình thang, \(\widehat{BAD}=\widehat{ABC}=90^o;AB=BC=a;AD=2a\), SA vuông góc với đáy và SA=2a. Gọi M, N lần lượt là trung điểm của SA và SD. Chứng minh rằng BCNM là hình chữ nhật và tính thể tích của khối chóp S.BCNM theo a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2022
\(\widehat{BAD}=120^0\Rightarrow\widehat{ABC}=60^0\Rightarrow\) các tam giác ABC và ACD là các tam giác đều
\(AH=AC\Rightarrow AH=AC=AB\Rightarrow\Delta HBC\) vuông tại B
\(\Rightarrow HB\perp BC\Rightarrow HB\perp AD\)
Qua H kẻ đường thẳng \(d\perp\left(ABCD\right)\Rightarrow S\in d\)
Gọi O là giao điểm AC và BD, do góc giữa (SBD) và đáy bằng 60 độ
\(\Rightarrow\widehat{SOH}=60^0\)
\(\Rightarrow SH=OH.tan60^0=\left(AH+AO\right).tan60=\left(a+\dfrac{a}{2}\right).tan60^0=\dfrac{3a\sqrt{3}}{2}\)
\(V_{S.ABCD}=\dfrac{1}{3}SH.S_{ABCD}=\dfrac{1}{3}.\dfrac{3a\sqrt{3}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2022
b.
\(SC=\sqrt{SH^2+HC^2}=\sqrt{SH^2+\left(2AC\right)^2}=\dfrac{a\sqrt{43}}{2}\)
\(\Rightarrow M\) là trung điểm SC \(\Rightarrow AM\) là đường trung bình tam giác SHC
\(\Rightarrow\left\{{}\begin{matrix}AM||SH\Rightarrow AM\perp\left(ABCD\right)\\AM=\dfrac{1}{2}SH=\dfrac{3a\sqrt{3}}{4}\end{matrix}\right.\)
\(HD=\sqrt{OD^2+OD^2}=\sqrt{\left(\dfrac{3a}{2}\right)^2+\left(\dfrac{a\sqrt{3}}{2}\right)^2}=a\sqrt{3}\)
\(\Rightarrow SD=\sqrt{SH^2+HD^2}=\dfrac{a\sqrt{39}}{2}\Rightarrow SN=\dfrac{1}{3}SD\Rightarrow ND=\dfrac{2}{3}SD\)
\(\Rightarrow d\left(N;\left(MAD\right)\right)=\dfrac{2}{3}d\left(S;\left(MAD\right)\right)\)
Mà \(SH||\left(MAD\right)\Rightarrow d\left(S;\left(MAD\right)\right)=d\left(H;\left(MAD\right)\right)\)
Gọi E là giao điểm BH và AD, ta có:
\(\left\{{}\begin{matrix}HB\perp AD\left(cmt\right)\\AM\perp\left(ABCD\right)\Rightarrow AM\perp HB\end{matrix}\right.\) \(\Rightarrow HB\perp\left(MAD\right)\)
\(\Rightarrow HE=d\left(H;\left(MAD\right)\right)\)
\(HE=\dfrac{1}{2}HB=\dfrac{1}{2}HD=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow d\left(N;\left(MAD\right)\right)=\dfrac{2}{3}HE=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow V_{AMND}=\dfrac{1}{3}.d\left(N;\left(MAD\right)\right).\dfrac{1}{2}AM.AD=\dfrac{a^3}{8}\)
28 tháng 3 2016
\(\widehat{BAD}=120^0\Rightarrow\widehat{ABC}\Rightarrow\Delta ABC\) đều
\(\Rightarrow AM=\frac{a\sqrt{3}}{2}\Rightarrow S_{ABCD}=\frac{a^3\sqrt{3}}{2}\)
Tam giác SAM vuông tại A có \(\widehat{SMA}=45^0\Rightarrow\) Tam giác SAM vuông tại A : SA = AM = \(\frac{a\sqrt{3}}{2}\)
Do đó \(V_{S.ABCD}=\frac{1}{3}SA.S_{ABCD}=\frac{a^3}{4}\)
Do AD song song với BC nên d(D;(SBC))=d(A,(SBC))
Gọi H là hình chiếu vuông góc của A trên SM
Ta có : \(\begin{cases}AM\perp BC\\SA\perp BC\end{cases}\)\(\Rightarrow BC\perp\cdot\left(SAM\right)\)
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow d\left(A,\left(SBC\right)\right)=AH\)
Ta có :
\(AH=\frac{AM\sqrt{2}}{2}=\frac{a\sqrt{6}}{4}\Rightarrow d\left(D,\left(SBC\right)\right)=\frac{a\sqrt{6}}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2023
B là khẳng định sai
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(CD=\left(SCD\right)\cap\left(BCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SDC) và (BCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{2}\Rightarrow\widehat{SDA}\approx54^044'\)
22 tháng 9 2023
Kẻ \(OI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right),OH \bot SI\left( {H \in SI} \right)\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot C{\rm{D}}\\OI \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SOI} \right)\\\left. \begin{array}{l} \Rightarrow C{\rm{D}} \bot OH\\OH \bot SI\end{array} \right\} \Rightarrow OH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {O,\left( {SC{\rm{D}}} \right)} \right) = OH\end{array}\)
\(\Delta ABC\) đều \( \Rightarrow AC = a \Rightarrow OC = \frac{1}{2}AC = \frac{a}{2}\)
\(\Delta ABD\) có \(\widehat {BA{\rm{D}}} = {120^ \circ } \Rightarrow B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2} - 2{\rm{A}}B.A{\rm{D}}} = a\sqrt 3 \Rightarrow OD = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta OCD\) vuông tại \(O\) có đường cao \(OI\)
\( \Rightarrow OI = \frac{{OC.O{\rm{D}}}}{{C{\rm{D}}}} = \frac{{a\sqrt 3 }}{4}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI \Rightarrow \Delta SOI\) vuông tại \(O\) có đường cao \(OH\)
\( \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {51} }}{{17}}\)
Vậy \(d\left( {O,\left( {SCD} \right)} \right) = OH = \frac{{a\sqrt {51} }}{{17}}\).
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2023
Gọi E là trung điểm BC \(\Rightarrow OE\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}AB=\dfrac{a}{2}\\OE||AB\Rightarrow OE\perp BC\end{matrix}\right.\)
\(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SEO\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SEO}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SEO}=\dfrac{SO}{OE}=\sqrt{3}\Rightarrow\widehat{SEO}=60^0\)
2 tháng 4 2016
Gọi I là trung điểm của AD.
Ta có : \(IA=ID=IC=a\Rightarrow CD\perp AC\)
Mặt khác, \(CD\perp SA\) suy ra CD vuông góc với SC nên tam giác SCD là tam giác vuông tại C
Trong tam giác vuông SAB ta có :
\(\frac{SH}{SB}=\frac{SA^2}{SB^2}=\frac{SA^2}{SA^2+AB^2}=\frac{2a^2}{2a^2+a^2}=\frac{2}{3}\)
Gọi \(d_{1,};d_2\) lần lượt là khoảng cách từ B và H đến mặt phẳng (SCD) thì
\(\frac{d_2}{d_1}=\frac{SH}{SB}=\frac{2}{3}\Rightarrow d_2=\frac{2}{3}d_1\)
\(d_1=\frac{3V_{B.SCD}}{S_{SCD}}=\frac{SA.S_{BCD}}{S_{SCD}}\)
\(S_{NCD}=\frac{1}{2}AB.BC=\frac{1}{2}a^2\)
\(S_{SCD}=\frac{1}{2}SC.CD=\frac{1}{2}\sqrt{SA^2+AB^2+BC^2}.\sqrt{IC^2+ID^2}=a^2\sqrt{2}\)
Suy ra \(d_1=\frac{a}{2}\)
Vậy khoảng cách từ H đến mặt phẳng (SCD) là \(d_2=\frac{2}{3}d_1=\frac{a}{3}\)
4 tháng 9 2018
Kẻ \(BH\perp CD\)
Mà \(CD\perp AD\left(gt\right)\Rightarrow BH//AD\)
Hình thang ABHD (AB//HD) có BH//AD nên \(\hept{\begin{cases}HD=AB=5\left(cm\right)\\BH=AD\end{cases}}\) (t/c hình thang)
\(HD+HC=DC\Rightarrow5+HC=9\Rightarrow HC=4\left(cm\right)\)
\(\Delta HBC\)vuông cân tại H nên \(HB=HC=4cm\Rightarrow AD=4cm\left(AD=BH\right)\)
Áp dụng định lí Pitago tính được \(BC=\sqrt{32}\left(cm\right)\)
Chu vi hình thang vuông ABCD là:
\(AB+BC+CD+AD=5+\sqrt{32}+9+4=18+\sqrt{32}\left(cm\right)\)
Chúc bạn học tốt.
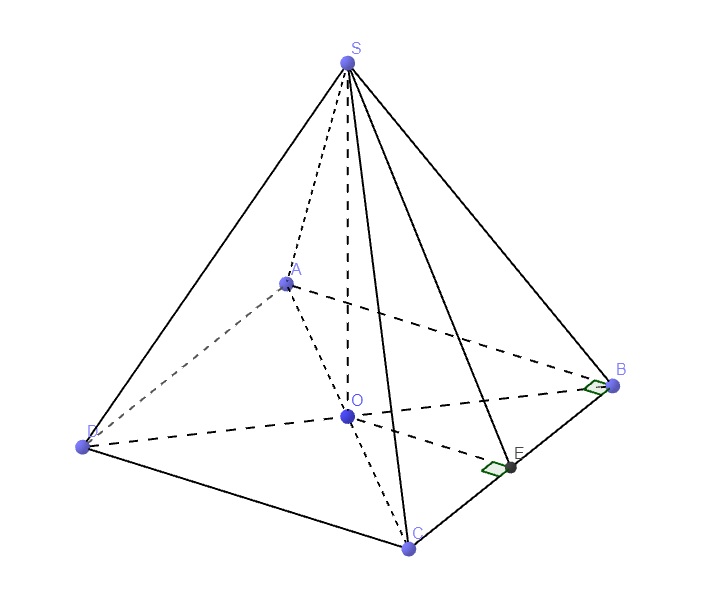
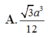
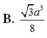
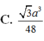
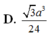
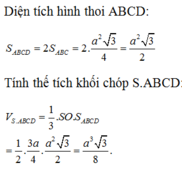
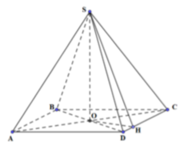
Ta có : MN là đường trung bình của tam giác SAD
Suy ra MN song song với AD và \(MN=\frac{1}{2}AD\Rightarrow\begin{cases}MN||BC\\MN=BC\end{cases}\)\(\Rightarrow\) BCNM là hình bình hành (1)
Mặt khác
\(\begin{cases}BC\perp AB\\BC\perp SA\end{cases}\)\(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp BM\left(2\right)\)
Từ (1) và (2) ra suy ra BCNM là hình chữ nhật
Ta có :
\(S_{BCNM}=2S_{\Delta BCM}\Rightarrow V_{S.BCNM}=2V_{S.BCM}\)
\(V_{S.BCM}=V_{C.SBM}=\frac{1}{3}CB.S_{\Delta SBM}=\frac{1}{6}CB.S_{\Delta SAB}=\frac{1}{6}CB.\frac{1}{2}SA.AB=\frac{a^3}{6}\)
Vậy \(V_{S.BCNM}=\frac{a^3}{3}\)