CHO x=2y;3y=2z
Tính A=x+y/y+z
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
DT
2
22 tháng 4 2020
Bài làm
Ta có: A = x2 - 2y + xy + 1 ; B = x2y - x2y2 - 1; C = - y - x2y2
=> A + B - C = ( x2 - 2y + xy + 1 ) + ( x2y - x2y2 - 1 ) - ( - y - x2y2 )
=> A + B - C = x2 - 2y + xy + 1 + x2y - x2y2 + y + x2y2
=> A + B - C = x2 + ( -2y + y ) + xy + ( -x2y2 + x2y2 ) + 1 + x2y
=> A + B - C = x2 - y + xy + 1 + x2y
Vậy A + B - C = x2 - y + xy + 1 + x2y
# Học tốt #
22 tháng 4 2020
Cho các đa thức: A= x^2- 2y +xy1; B=x^2 + y-x^2y^2-1; C=-y- x^2y^2. Tính A+B-C
#giúp mik làm bài kiểu này vs ạ
DK
Biết x-2y=5. Giá trị biểu thức A=x(2y-x)+2y(x-2y) là.....
Ai giải xong tr và đúng nhất mình tick cho
1
VN
16 tháng 3 2017
Thử nhé.
A = x(2y-x) + 2y(x-2y)
A = 2y + 5 . (-5) + 2y.5
A = -10y - 25 + 10y
A = -25
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 8 2021
\(VT=\dfrac{2y+3z+5}{1+x}+1+\dfrac{3z+x+5}{2y+1}+1+\dfrac{x+2y+5}{1+3z}+1-3\)
\(VT=\dfrac{x+2y+3z+6}{1+x}+\dfrac{x+2y+3z+6}{1+2y}+\dfrac{x+2y+3z+6}{1+3z}-3\)
\(VT=24\left(\dfrac{1}{1+x}+\dfrac{1}{1+2y}+\dfrac{1}{1+3z}\right)-3\ge\dfrac{24.9}{1+x+1+2y+1+3z}-3=\dfrac{216}{21}-3=\dfrac{51}{7}\)
CM
30 tháng 3 2017
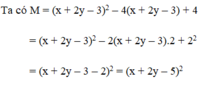
Ta có: x - 4 = -2y hay x + 2y = 4
Thay x + 2y = 4 vào M ta được
M = 4 - 5 2 = - 1 2 = 1
Vậy M = 1
Đáp án cần chọn là C
T
0
(Try!)
Ta có: \(3y=2z\Rightarrow\frac{y}{2}=\frac{z}{3}\Rightarrow z=\frac{3y}{2}\)
Thế vào có: \(\frac{x+y}{y+z}=\frac{2y+y}{\frac{3y}{2}+y}=\frac{3y}{\frac{3y+2y}{2}}=\frac{3y}{\frac{5y}{2}}\)
Bạn nhầm một chỗ rồi 3x=2y chứ không phải x=2y nha!Bạn giúp mình làm lại nhé!