Có bao nhiêu số nguyên m ∈ (-20; 20) để hàm số y = (x2 + 2)\(\left|x^2-m\right|\) có đúng 5 điểm cực trị
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
30 tháng 1 2018
Chọn đáp án B.
![]()
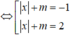
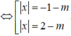
Phương trình có bốn nghiệm thực phân biệt
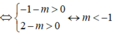
![]()
Vậy có tất cả 18 số nguyên thoả mãn.

6 tháng 3 2016
Có bao nhiêu số nguyên tố nhỏ hơn 20
Có 8 số nguyên tố nhỏ hơn 20

LV
9 tháng 8 2016
Có 4 phân số bằng phân số -15/20
Đó là : -3/4 ; -6/8 ; -9/12 ; -12/16
Ủng hộ nha
18 tháng 3 2017
Bạn ơi có 4 phân số bằng phân số -15/20 đó là:
-3/4; -6/8; -9/12; -12/16.
Nhớ kết bạn với mình nha Nalumi Likika

ML
2 tháng 4 2021
program hoc24;
n: string[20];
k,i,t,d,d1: byte;
code: integer;
begin
write('Nhap so K: '); readln(k);
write('Nhap so nguyen N: '); readln(n);
d:=0; d1:=0;
for i:=1 to k do
begin
val(n[i],t,code);
if t mod 2=0 then d:=d+1 else d1:=d1+1;
end;
writeln('Co ',d,' chu so chan');
write('Co ',d1,' chu so le');
readln
end.
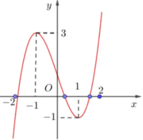
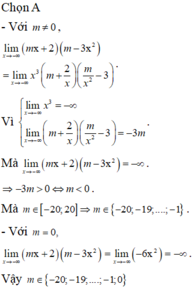
Lưu ý rằng \(x^2+2>0\) với mọi x, do đó \(x^2+2=\left|x^2+2\right|\):
\(y=\left(x^2+2\right)\left|x^2-m\right|=\left|\left(x^2+2\right)\left(x^2-m\right)\right|\)
Tới đây là 1 bài biện luận cực trị của hàm trị tuyệt đối trùng phương khá cơ bản:
\(g\left(x\right)=\left(x^2+2\right)\left(x^2-m\right)=x^4-\left(m-2\right)x^2-2m\)
\(g'\left(x\right)=4x^3-2\left(m-2\right)x=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=\dfrac{m-2}{2}\end{matrix}\right.\)
Do \(g\left(x\right)=0\Leftrightarrow\left(x^2+2\right)\left(x^2-m\right)=0\Leftrightarrow x^2=m\) có tối đa 2 nghiệm
Đồng thời \(g'\left(x\right)=0\) có tối đa 3 nghiệm
\(\Rightarrow\) Hàm có 5 cực trị khi và chỉ khi \(g\left(x\right)=0\) có 2 nghiệm pb đồng thời \(g'\left(x\right)=0\) có 3 nghiệm pb và các nghiệm này ko trùng nhau
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\dfrac{m-2}{2}>0\\m\ne\dfrac{m-2}{2}\end{matrix}\right.\) \(\Leftrightarrow m>2\)
có đứa bạn mình làm theo hướng là đạo hàm ngay từ đầu, nếu làm cách đó thì có nhanh hay dễ tư duy hơn không???