Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đơn giản là bạn vẽ cái hàm bậc 4 đó ra và cho -m và -m-10 cắt thôi. Vì -m-10<-m nên -m-10 sẽ nằm ở dưới, còn -m nằm trên. Nên -m sẽ cắt 2 điểm và -m-10 cắt 4 điểm cho ta 6 điểm. Ngoài ra k còn trường hợp nào khác mà -m và -m-10 cắt thỏa mãn

Xét hàm \(f\left(x\right)=x^5-5x^3-20x+m\)
\(f'\left(x\right)=5x^4-15x^2-20=0\) có 2 nghiệm
\(\Rightarrow f\left(x\right)\) có 2 cực trị
\(\Rightarrow y=\left|f\left(x\right)\right|\) có 5 cực trị khi \(x^5-5x^3-20x+m=0\) có 3 nghiệm bội lẻ
Từ BBT ta thấy \(y=-m\) cắt \(y=x^5-5x^3-20x\) tại 3 điểm pb khi và chỉ khi:
\(-48\le-m\le48\Rightarrow-48\le m\le48\)
\(\Rightarrow\) Có 97 giá trị nguyên của m

\(g\left(x\right)=3x^4-4x^3-6mx^2+12mx\)
\(g'\left(x\right)=12x^3-12x^2-12mx+12m=0\)
\(\Leftrightarrow12x^2\left(x-1\right)-12m\left(x-1\right)=0\)
\(\Leftrightarrow12\left(x^2-m\right)\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x^2=m\end{matrix}\right.\)
Xét \(g\left(x\right)=0\Leftrightarrow x\left(3x^3-4x^2-6mx+12m\right)=0\)
- Nếu \(m=0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ \(\Rightarrow f\left(x\right)\) có 3 cực trị (thỏa mãn)
- Nếu \(m=\dfrac{1}{6}\Rightarrow g'\left(x\right)=0\) có 3 nghiệm bội lẻ, \(g\left(x\right)=0\) có 3 nghiệm pb nhưng chỉ có 1 nghiệm \(x=1\) trùng với \(g'\left(x\right)=0\) nên hàm có 5 cực trị (ktm)
- Nếu \(m=1\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (thỏa mãn)
- Nếu \(m< 0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ \(x=1\)
Khi đó hàm có 3 cực trị khi \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (hiển nhiên từ các TH này thì \(g\left(x\right)=0\) ko thể có nghiệm \(x=1\) do đã loại trừ từ TH \(m=\dfrac{1}{6}\))
\(\Leftrightarrow3x^3-4x^2-6mx+12m=0\) có đúng 1 nghiệm
\(\Leftrightarrow3x^3-4x^2=6m\left(x-2\right)\Leftrightarrow m=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) (do \(x=2\) ko là nghiệm)
Khảo sat \(h\left(x\right)=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) ta được \(y=m\) cắt \(y=h\left(x\right)\) tại đúng 1 điểm khi: \(\left[{}\begin{matrix}m< 0\\\dfrac{1}{6}< m< \dfrac{64}{9}\\\end{matrix}\right.\) \(\Leftrightarrow m< 0\)
- Nếu \(m>0;m\ne\left\{\dfrac{1}{6};1\right\}\) \(\Rightarrow g'\left(x\right)=0\) có 3 nghiệm pb
Mà \(g\left(x\right)=0\) luôn có ít nhất 1 nghiệm bội lẻ \(x=0\)
\(\Rightarrow\) Hàm có 3 cực trị khi và chỉ khi:
TH1: \(3x^3-4x^2-6mx+12m=0\) vô nghiệm (vô lý do hàm bậc 3 luôn có nghiệm)
Th2: \(3x^3-4x^2-6mx+12m=0\) (1) có 3 nghiệm đều trùng với nghiệm của \(g'\left(x\right)=0\) (vô lý do \(m\ne\dfrac{1}{6}\) nên nếu (1) có nghiệm thì nó luôn có nghiệm khác 1)
Kết luận: \(\left[{}\begin{matrix}m=1\\m\le0\end{matrix}\right.\)
lúc đầu mk giải câu này theo kiểu xét 3 trường hợp là m < 0; 1 nằm giữa hai nghiệm kia; 1 nằm bên phải 2 nghiệm kia. Không biêt cách này có đúng không mà tính ra kết quả là 10 giá trị ???

- Với \(m=1\) thỏa mãn
- Với \(m\ne1\):
\(f'\left(x\right)=3\left(m-1\right)x^2-10x+m+3\)
\(f\left(\left|x\right|\right)\) có số cực trị bằng \(2k+1\) với \(k\) là số cực trị dương của \(f\left(x\right)\) nên hàm có 3 cực trị khi \(f'\left(x\right)=0\) có đúng 1 nghiệm dương
TH1: \(f'\left(x\right)=0\) có 1 nghiệm bằng 0 \(\Rightarrow m=-3\Rightarrow f'\left(x\right)=-12x^2-10x\) ko có nghiệm dương (loại)
TH2: \(f'\left(x\right)=0\) ko có nghiệm bằng 0 nào \(\Rightarrow f'\left(x\right)=0\) khi và chỉ khi nó có 2 nghiệm trái dấu
\(\Rightarrow ac< 0\Leftrightarrow3\left(m-1\right)\left(m+3\right)< 0\)
\(\Rightarrow-3< m< 1\)
Vậy \(-3< m\le1\)

Đề đúng là \(y=mx^2+2\left(m^2-5\right)x^4+4\) chứ bạn (nghĩa là ko bị nhầm lẫn vị trí \(x^2\) và \(x^4\))
Hàm có đúng 2 điểm cực đại và 1 điểm cực tiểu khi:
\(\left\{{}\begin{matrix}2\left(m^2-5\right)< 0\\2\left(m^2-5\right).m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \sqrt{5}\)
\(\Rightarrow\) có 2 giá trị nguyên của m thỏa mãn

Gọi số điểm cực trị dương của \(f\left(x\right)\) là k thì số cực trị của \(f\left(\left|x\right|\right)\) là \(2k+1\)
Do đó để \(g\left(x\right)\) có 5 cực trị thì \(f'\left(x\right)=0\) có 2 nghiệm dương
\(\Rightarrow x^2+2mx+5=0\) có 2 nghiệm dương phân biệt
\(\Rightarrow\left\{{}\begin{matrix}\Delta'=m^2-5>0\\x_1+x_2=-2m>0\\x_1x_2=5>0\end{matrix}\right.\) \(\Rightarrow m< -\sqrt{5}\)
\(\Rightarrow m=\left\{-3;-4;-5;...;-9\right\}\)



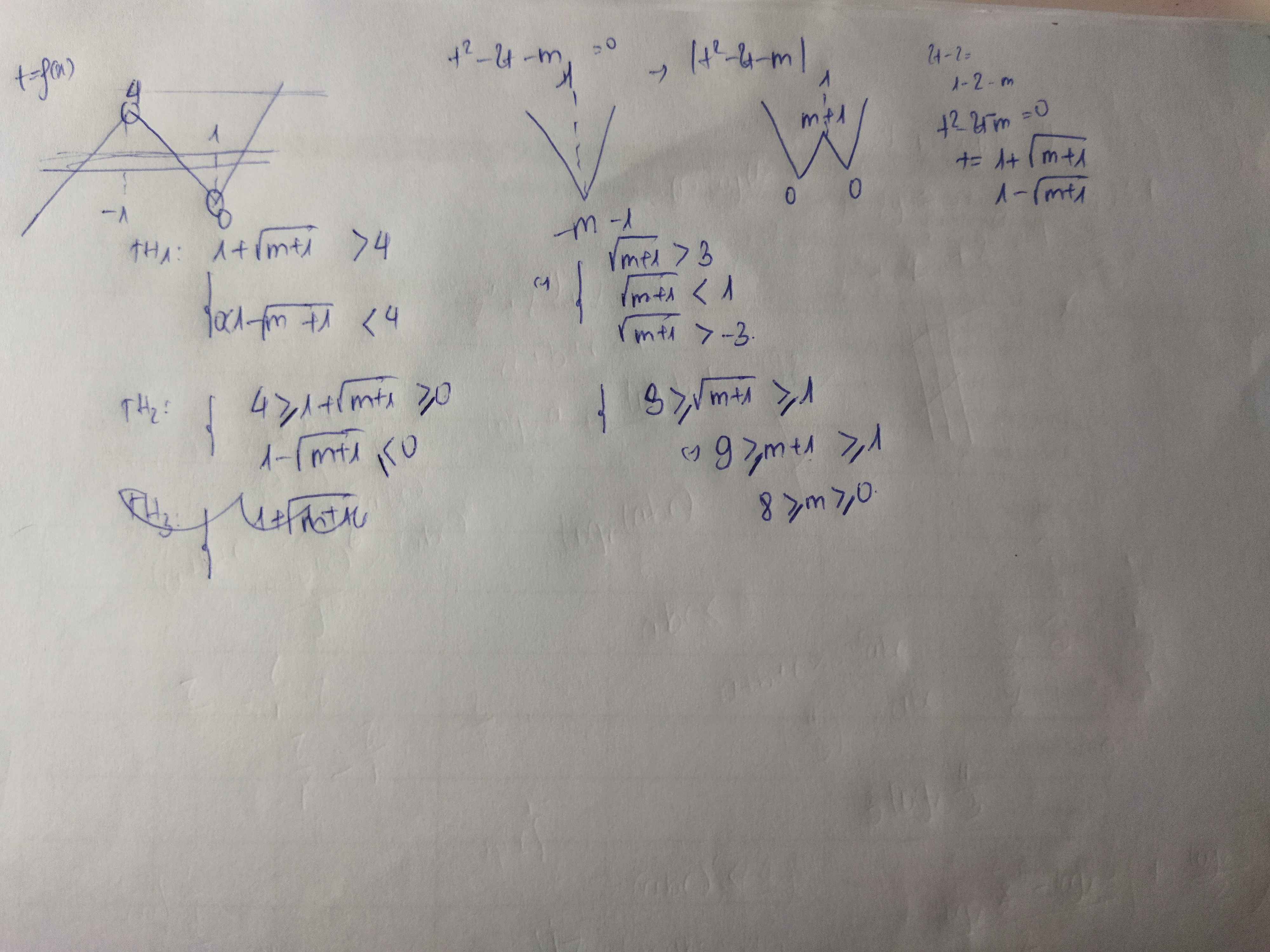 9 đko nhỉ
9 đko nhỉ
Lưu ý rằng \(x^2+2>0\) với mọi x, do đó \(x^2+2=\left|x^2+2\right|\):
\(y=\left(x^2+2\right)\left|x^2-m\right|=\left|\left(x^2+2\right)\left(x^2-m\right)\right|\)
Tới đây là 1 bài biện luận cực trị của hàm trị tuyệt đối trùng phương khá cơ bản:
\(g\left(x\right)=\left(x^2+2\right)\left(x^2-m\right)=x^4-\left(m-2\right)x^2-2m\)
\(g'\left(x\right)=4x^3-2\left(m-2\right)x=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=\dfrac{m-2}{2}\end{matrix}\right.\)
Do \(g\left(x\right)=0\Leftrightarrow\left(x^2+2\right)\left(x^2-m\right)=0\Leftrightarrow x^2=m\) có tối đa 2 nghiệm
Đồng thời \(g'\left(x\right)=0\) có tối đa 3 nghiệm
\(\Rightarrow\) Hàm có 5 cực trị khi và chỉ khi \(g\left(x\right)=0\) có 2 nghiệm pb đồng thời \(g'\left(x\right)=0\) có 3 nghiệm pb và các nghiệm này ko trùng nhau
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\dfrac{m-2}{2}>0\\m\ne\dfrac{m-2}{2}\end{matrix}\right.\) \(\Leftrightarrow m>2\)
có đứa bạn mình làm theo hướng là đạo hàm ngay từ đầu, nếu làm cách đó thì có nhanh hay dễ tư duy hơn không???