Trong mặt phẳng Oxy , cho ba điểm A ( 2 ; -1 ) , B ( 3 ; -6 ) , C ( -2 ; 1 )
1) Tìm tọa độ điểm D để ABCD là hình bình hành .
2 ) Tìm tọa độ M sao cho \(\overrightarrow{MA}=2\overrightarrow{MB}-\overrightarrow{MC}\)
3 ) Tìm tọa độ điểm E trên trục Ox để \(\left|\overrightarrow{EA}+\overrightarrow{EB}+2\overrightarrow{EC}\right|\) nhỏ nhất .
HELP ME...
Đọc tiếp
Trong mặt phẳng Oxy , cho ba điểm A ( 2 ; -1 ) , B ( 3 ; -6 ) , C ( -2 ; 1 )
1) Tìm tọa độ điểm D để ABCD là hình bình hành .
2 ) Tìm tọa độ M sao cho \(\overrightarrow{MA}=2\overrightarrow{MB}-\overrightarrow{MC}\)
3 ) Tìm tọa độ điểm E trên trục Ox để \(\left|\overrightarrow{EA}+\overrightarrow{EB}+2\overrightarrow{EC}\right|\) nhỏ nhất .
HELP ME !!!!!
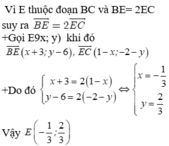
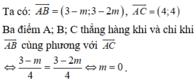
Bạn ghi cho đúng môn học nhé !
1) ABCD là HBH thì:
\(\overrightarrow{AB}=\overrightarrow{DC}\)\(\Leftrightarrow\) \(\left(1;-5\right)=\left(-2-x_D;1-y_D\right)\)
\(\Leftrightarrow\) \(\hept{\begin{cases}-2-x_D=1\\1-y_D=-5\end{cases}}\)\(\Leftrightarrow\) \(\hept{\begin{cases}x_D=-3\\y_D=6\end{cases}}\)
2) Bạn chuyển hết vế phải qua vế trái
Xác định tọa độ các vecto MA MB MC (nhân với các hệ số tương ứng)
thì ta có được hpt:
\(\hept{\begin{cases}x_{MA}-2x_{MB}+x_{MC}=0\\y_{MA}-2y_{MB}+y_{MC}=0\end{cases}}\)
Bạn tự làm tiếp nhé
Mình cảm ơn