Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Để chứng minh A,B,C là 3 đỉnh của tam giác cần chứng minh
\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)
Thật vậy: \(\left(x_B-x_A;y_B-y_A\right)+\left(x_C-x_B;y_C-y_B\right)=\left(x_C-x_A;y_C-y_A\right)\)
\(\Leftrightarrow\left(-3-6;6-3\right)+\left(1+3;-2-6\right)=\left(1-6;-2-3\right)\)
\(\Leftrightarrow\left(-5;-5\right)=\left(-5;-5\right)\)
Vậy ...
b/ Để A,B,D thẳng hàng<=> \(\overrightarrow{AB}=x\overrightarrow{AD}\)
Vì D nằm trên trục hoành nên yD= 0
\(\Leftrightarrow\left(x_B-x_A;y_B-y_A\right)=x\left(x_D-x_A;y_D-y_A\right)\)
\(\Leftrightarrow\left(-9;3\right)=x\left(x_D-6;y_D-3\right)\)
\(\left\{{}\begin{matrix}x\left(x_D-6\right)=-9\\-3x=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\x_D=9+6=15\end{matrix}\right.\)
\(\Rightarrow D\left(15;0\right)\)
c/ \(E\in BC\Rightarrow\overrightarrow{BE}=2\overrightarrow{EC}\)
\(\Leftrightarrow\left(x_E-x_B;y_E-y_B\right)=2\left(x_C-x_E;y_C-y_E\right)\)
\(\Leftrightarrow\left(x_E+3;y_E-6\right)=2\left(1-x_E;-2-y_E\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}3+x_E=2-2x_E\\y_E-6=-4-2y_E\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_E=-\frac{1}{3}\\y_E=\frac{2}{3}\end{matrix}\right.\Rightarrow E\left(-\frac{1}{3};\frac{2}{3}\right)\)
d/ Gọi pt đt DE có dạng: \(\left(d_1\right)y=ax+b\)
Vì \(D,E\in\left(d_1\right)\Rightarrow\left\{{}\begin{matrix}15a+b=0\\-\frac{1}{3}a+b=\frac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\frac{1}{23}\\b=\frac{15}{23}\end{matrix}\right.\)
\(\Rightarrow\left(d_1\right)y=-\frac{1}{23}x+\frac{15}{23}\)
Gọi pt đt AC có dạng: \(\left(d_2\right)y=ax+b\)
Vì \(A,C\in\left(d_2\right)\Rightarrow\left\{{}\begin{matrix}6a+b=3\\a+b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-3\end{matrix}\right.\)
\(\Rightarrow\left(d_2\right)y=x-3\)
Bạn tự xét PTHĐGĐ của (d1) và (d2)

Hình chữ nhật ADN gì bạn nhỉ?
Hình chữ nhật phải có 4 đỉnh

E trên trục hoành nên E(x;0)
A(6;3); B(-3;6); E(x;0)
\(\overrightarrow{AB}=\left(-9;3\right);\overrightarrow{AE}=\left(x-6;-3\right)\)
Để A,B,E thẳng hàng thì \(\dfrac{x-6}{-9}=\dfrac{-3}{3}=-1\)
=>x-6=9
=>x=15
Vậy: E(15;0)
Do E thuộc trục hoành nên tọa độ có dạng \(E\left(x;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-9;3\right)\\\overrightarrow{AE}=\left(x-6;-3\right)\end{matrix}\right.\)
3 điểm A, B, E thẳng hàng khi:
\(\dfrac{x-6}{-9}=\dfrac{-3}{3}\Rightarrow x-6=9\)
\(\Rightarrow x=15\Rightarrow E\left(15;0\right)\)

a: A(2;4); B(1;0); C(2;2)
vecto AB=(-1;-4)
vecto DC=(2-x;2-y)
Vì ABCD là hình bình hành nên vecto AB=vecto DC
=>2-x=-1 và 2-y=-4
=>x=3 và y=6
c: N đối xứng B qua C
=>x+1=4 và y+0=4
=>x=3 và y=4

Chọn D.
Gọi điểm M có tọa độ là ( x; y)
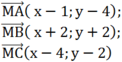
MA2 + 2MB2 + 3MC2
= (x - 1)2 + (y - 4)2 + 2[ (x + 2)2 + (y + 2)2] + 3[ (x - 4)2 + (y - 2)2]
= 6x2-18x + 6y2 + 93 = 1,5. (2x - 3)2 + 6(y - 1)2 + 147/2 ≥ 147/2
Dấu “=” xảy ra khi x = 1,5 và y = 1
Vậy tọa độ điểm M cần tìm là ( 1,5; 1).
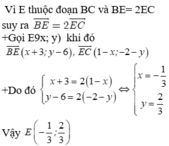
Ý của đề bài là điểm E nằm trên đoạn BC chứ không phải trên đường thẳng BC đúng không nhỉ?
Gọi \(E\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{BE}=\left(x+3;y-6\right)\\\overrightarrow{EC}=\left(1-x;-2-y\right)\end{matrix}\right.\)
\(\overrightarrow{BE}=2\overrightarrow{EC}\Rightarrow\left\{{}\begin{matrix}x+3=2\left(1-x\right)\\y-6=2\left(-2-y\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\frac{1}{3}\\y=\frac{2}{3}\end{matrix}\right.\) \(\Rightarrow E\left(-\frac{1}{3};\frac{2}{3}\right)\)