Cho hàm số y=f(x) có các đạo hàm cấp một và đạo hàm cấp hai liên tục trên [0;1] và thỏa mản hệ thức \(\int\limits^1_0e^xf\left(x\right)dx=\int\limits^1_0e^xf'\left(x\right)dx=\int\limits^1_0e^xf''\left(x\right)dx\ne0\). Tính giá trị của biểu thức:\(\frac{ef'\left(1\right)-f'\left(0\right)}{ef\left(1\right)-f\left(0\right)}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 11 2019
Đáp án C
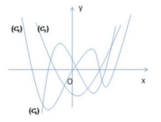
Dựa vào hình vẽ, ta thấy rằng:
Đồ thị C 3 có dạng đồ thị hàm số trùng phương.
Đồ thị C 2 có dạng đồ thị hàm số bậc hai (parabol)
Đồ thị C 1 có dạng đồ thị hàm số bậc ba
Vậy đồ thị của các hàm số
.
.
.
.
.
CM
9 tháng 5 2018
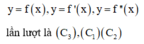
Chọn A
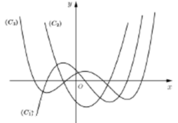
Gọi hàm số của các đồ thị 
tương ứng là 
.
Ta thấy đồ thị 
có các điểm cực trị có hoành độ là nghiệm của phương trình 
nên hàm số 
là đạo hàm của hàm số 
.
Đồ thị 
có các điểm cực trị có hoành độ là nghiệm của phương trình 
nên hàm số 
là đạo hàm của hàm số 
.
Vậy, đồ thị các hàm số 
, 
và 
theo thứ tự, lần lượt tương ứng với đường cong 
.
CM
30 tháng 11 2017
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
CM
10 tháng 10 2019
Đáp án D
∫ 0 1 e x f x d x = ∫ 0 1 e x f ' x d x = ∫ 0 1 e x f ' ' x d x = k ≠ 0
Đặt
u = e x d v = f ' x d x ⇒ d u = e x d x v = f x ⇒ ∫ 0 1 e x f ' x d x = e x f x 0 1 − ∫ 0 1 e x f x d x
⇒ k = e . f 1 − f 0 − k ⇒ e f 1 − f 0 = 2 k .
Đặt
u = e x d v = f ' ' x d x ⇒ d u = e x d x v = f ' x ⇒ ∫ 0 1 e x f ' ' x d x = e x f ' x 0 1 − ∫ 0 1 e x f ' x d x
⇒ k = e . f ' 1 − f ' 0 − k ⇒ e . f ' 1 − f ' 0 = 2 k .
Vậy e . f ' 1 − f ' 0 e . f 1 − f 0 = 2 k 2 k = 1
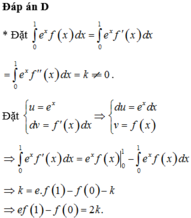
Xét tích phân \(I=\int\limits^1_0e^xf\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=e^x.f\left(x\right)|^1_0-\int\limits^1_0e^xf'\left(x\right)dx=e.f\left(1\right)-f\left(0\right)-I\)
\(\Rightarrow2I=e.f\left(1\right)-f\left(0\right)\)
Xét tích phân \(J=\int\limits^1_0f'\left(x\right)dx=I\)
Đặt \(\left\{{}\begin{matrix}u=f'\left(x\right)\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f''\left(x\right)dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=J=e^x.f'\left(x\right)|^1_0-\int\limits^1_0e^x.f''\left(x\right)dx=e.f'\left(1\right)-f'\left(0\right)-I\)
\(\Rightarrow2I=e.f'\left(1\right)-f'\left(0\right)\)
\(\Rightarrow\frac{e.f'\left(1\right)-f'\left(0\right)}{e.f\left(1\right)-f\left(0\right)}=\frac{2I}{2I}=1\)