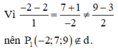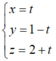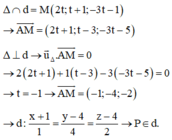Trong không gian Oxyz, đường thẳng (d) đi qua điểm và nhận vectơ làm vectơ chỉ phương có phương trình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Đường thẳng d đi qua F(0;1;2) vì thay tọa độ F vào phương trình d ta được 1 giá trị t=0.

Ta có: a d → = (2; −1; 4)
Xét điểm B(–3 + 2t; 1 – t; –1 + 4t) thì AB → = (1 + 2t; 3 − t; −5 + 4t)
AB ⊥ d ⇔ AB → . a d → = 0
⇔ 2(1 + 2t) − (3 − t) + 4(−5 + 4t) = 0 ⇔ t = 1
Suy ra AB → = (3; 2; −1)
Vậy phương trình của
∆
là 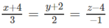

Chọn đáp án D
Cách 1: Thay tọa độ điểm M vào phương trình của d

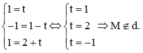
Thay tọa độ điểm N vào phương trình của d.
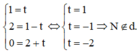
Thay tọa độ điểm P vào phương trình của d.
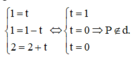
Vậy Thật vậy, thay tọa độ điểm Q vào phương trình d
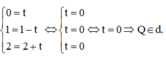
Cách 2: Quan sát thấy ba điểm M, N, P đều có hoành độ bằng 1.
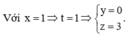
Suy ra M, N, P đều không thuộc d. Do đó đáp án đúng là D.

Đáp án D
Phương pháp

Viết phương trình đường thẳng biết điểm đi qua và VTCP
Cách giải
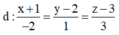
![]()
∆ vuông góc với d và AB => AB nhận u → = ( - 2 ; 1 ; 3 ) và A B → = ( - 2 ; 3 ; 2 ) là cặp VTPT
![]()
Phương trình đường thẳng
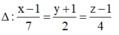

Đáp án D
Phương pháp: △ ⊥ d △ ⊥ A B ⇒ u △ → = u d → ; A B →
Viết phương trình đường thẳng biết điểm đi qua và VTCP.
Cách giải: d; x + 1 - 2 = y - 2 1 = z - 3 3 có 1 VTCP u → - 2 ; 1 ; 3 ; A B → = - 2 ; 3 ; 2
∆ vuông góc với d và AB => AB nhận u → - 2 ; 1 ; 3 và A B → = - 2 ; 3 ; 2 là cặp VTPT
=> ∆ có 1 VTCP v → = A B → ; u → = ( 7 ; 2 ; 4 )
Phương trình đường thẳng ∆: x - 1 7 = y + 1 2 = z - 1 4