Xác định Parabol (P): y = ax 2 + bx + 3 biết rằng Parabol có đỉnh I (3; -2)
A. y = x 2 − 6 x + 3
B. y = − 5 9 x 2 + 10 3 x + 3
C. y = 3 x 2 + 9 x + 3
D. y = 5 9 x 2 − 10 3 x + 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề bài thiếu, không thể xác định chính xác (P) khi chỉ biết đỉnh

Parabol y = ax2 + bx + 2 có đỉnh I(2 ; –2), suy ra :
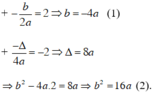
Từ (1) ⇒ b2 = 16.a2, thay vào (2) ta được 16a2 = 16a ⇒ a = 1 ⇒ b = –4.
Vậy parabol cần tìm là y = x2 – 4x + 2.

Đỉnh của parabol là \(\frac{-\Delta}{4a}\) ta có
\(\left\{{}\begin{matrix}\frac{-\Delta}{4a}=-25\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\24a+c=0\\2a+b=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4a^2-4ac=100a\\24a+c=0\\b=-2a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-c=25\\24a+c=0\\b=-2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=-24\end{matrix}\right.\)
\(\Rightarrow y=x^2-2x-24\)

Đồ thị hàm số \(y = a{x^2} + bx + c\) đi qua điểm A(8; 0) nên:
\(a{.8^2} + b.8 + c = 0 \Leftrightarrow 64a + 8b + c = 0\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh là I(6;-12):
\(\frac{{ - b}}{{2a}} = 6 \Leftrightarrow - b = 12a \Leftrightarrow 12a + b = 0\)
\(a{.6^2} + 6b + c = - 12 \Leftrightarrow 36a + 6b + c = - 12\)
Từ 3 phương trình trên ta có: \(a = 3;b = - 36,c = 96\)
=> Hàm số cần tìm là \(y = 3{x^2} - 36x + 96\)

\(a,\Leftrightarrow\left\{{}\begin{matrix}9a+3b=-6\\\dfrac{b}{2a}=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+b=-2\\3a=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{3}\\b=-1\end{matrix}\right.\\ \Leftrightarrow\left(P\right):y=-\dfrac{1}{3}x^2-x+2\\ b,\Leftrightarrow\left\{{}\begin{matrix}4a+2b=-3\\-\dfrac{b}{2a}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a+2b=-3\\4a-b=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{4}\\b=-1\end{matrix}\right.\Leftrightarrow\left(P\right):y=-\dfrac{1}{4}x^2-x+2\)
Đáp án D