Với mỗi trường hợp sau, hãy đoán xem đơn thức A có chia hết cho đơn thức B không; nếu chia hết, hãy tìm thương của phép chia A cho B và giải thích cách làm:
a) \(A = 6{x^3}y,B = 3{x^2}y\)
b) \(A = {x^2}y,B = x{y^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 8 2019
Hạng tử y 6 của đa thức A không chia hết cho đơn thức B = 2x.
Do đó, đa thức A không chia hết cho đơn thức B
Chọn đáp án A
CM
31 tháng 7 2019
Nhận thấy:
15xy2 chia hết cho 6y2
17xy3 chia hết cho 6y2
18y2 chia hết cho 6y2
Vậy A = 15xy2 + 17xy3 + 18y2 chia hết cho 6y2 hay A chia hết cho B.
HQ
Hà Quang Minh
Giáo viên
12 tháng 1 2024
a) Không vì hạng tử \( 9x{y^4}\) có số mũ của biến x nhỏ hơn số mũ của biến x trong B.
b) Có. \(\begin{array}{l}A:B = \left( {9x{y^4} - 12{x^2}{y^3} + 6{x^3}{y^2}} \right):\left( { - 3x{y^2}} \right)\\ = 9x{y^4}:\left( { - 3x{y^2}} \right) - 12{x^2}{y^3}:\left( { - 3x{y^2}} \right) + 6{x^3}{y^2}:\left( { - 3x{y^2}} \right)\\ = - 3{y^2} + 4xy - 2{x^2}\end{array}\)
20 tháng 4 2017
Bài giải:
A chia hết cho B vì mỗi hạng tử của A đều chia hết cho B (mỗi hạng tử của A đều có chứa nhân tử y với số mũ lớn hơn hay bằng 2 bằng với số mũ của y trong B).
CM
19 tháng 6 2017
Lời giải của bạn Hà sai, lời giải của bạn Quang đúng.
Vì 5x4 chia hết cho 2x2;
–4x3 chia hết cho 2x2;
6x2y chia hết cho 2x2
Do đó A = 5x4 – 4x3 + 6x2y chia hết cho 2x2 hay A chia hết cho B.
Chú ý: Đơn thức A chia hết cho đơn thức B nếu tìm được đơn thức Q sao cho A=B.Q
Ví dụ : Cho hai đơn thức A= 2x2y3; B = 7xy
Khi đó với đơn thức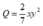 
thì A=B.Q
Do đó, đơn thức A chia hết cho đơn thức B.
DN
21 tháng 7 2017
vì các hạng tử của đa thức A chia hết cho đơn thức B nên A chia hết cho B
21 tháng 1 2018
a) nếu a,b là hằng thì A là đơn thức
đơn thức A có hệ số \(\frac{-4a}{\left(b+1\right)^3}\); có bậc 2 đối với x, có bậc 5 đối với y và có bậc 7 đối với tập hợp các biến
b) Nếu chỉ có a là hằng thì A không phải đơn thức vì A có chứa phép chia, phép cộng đối với biến b
c) Nếu b là hằng thì A là đơn thức
Đơn thức A có hệ số là \(\frac{-4a}{\left(b+1\right)^3}\), có bậc 1 đối với a ; bậc 2 đối với x ; bậc 5 đối với y và có bậc 8 đối với tập hợp các biến
a) Đơn thức A chia hết cho đơn thức B:
\(A:B = 6{x^3}y:3{x^2}y = \left( {6:3} \right).\left( {{x^3}:{x^2}} \right).\left( {y:y} \right) = 2x\)
b) Đơn thức A không chia hết cho đơn thức B vì số mũ của biến y trong B lớn hơn số mũ của biến y trong A.