Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài giải:
Ta có: A : B = (5x4 – 4x3 + 6x2y) : 2x2
= (5x2 : 2x2) + (– 4x3 : 2x2) + (6x2y : 2x2)
= 5252x2 – 2x + 3y
Như vậy A chia hết cho B vì mọi hạng tử của A đều chia hết cho B.
Vậy: Quang trả lời đùng, Hà trả lời sai.
Ta có: A : B = (5x4 – 4x3 + 6x2y) : 2x2
= (5x2 : 2x2) + (– 4x3 : 2x2) + (6x2y : 2x2)
= 5252x2 – 2x + 3y
Như vậy A chia hết cho B vì mọi hạng tử của A đều chia hết cho B.
Vậy: Quang trả lời đùng, Hà trả lời sai.
Bài giải:
A chia hết cho B vì mỗi hạng tử của A đều chia hết cho B (mỗi hạng tử của A đều có chứa nhân tử y với số mũ lớn hơn hay bằng 2 bằng với số mũ của y trong B).
a) A chia hết cho B vì x4, x3, x2 đều chia hết cho x2
b) A chia hết cho B, vì x2– 2x + 1 = (1 – x)2, chia hết cho 1 - x
a) ta có:
x3-3x+5x-6=x3-x2+3x-2x2+2x-6
=x.(x2-x+3)-2.(x2-x+3)
=(x2-x+3)(x-2)
Vậy x3-3x2+5x-6 chia hết cho x-2
b)ta có:
x3-3x2+5x-6=x3-5x2+15x+2x2-10x+30-36
=x.(x2-5x+15)+2.(x2-5x+15)-36
=(x2-5x+15)(x+2)-36
Vậy x3-3x2+5x-6 chia cho x+2 được thương là x2-5x+15 dư -36
Thôi làm đa thức B trước cho dễ làm:
Ta có \(B=\left(3x+1\right)^2-x\left(5x+2\right)+3\)
\(=\left(3x\right)^2+2.3.x+1+1^2-5x^2-2x+3\)
\(=9x^2+6x+1-5x^2-2x+3\)
\(=4x^2+4x+4\)
\(=4\left(x^2+x+1\right)\)
\(A=x^{2016}-x^{2013}+x^2+x+1\)
\(=x^{2013}\left(x^3-1\right)+\left(x^2+x+1\right)\)
\(=x^{2013}\left(x-1\right)\left(x^2+x+1^2\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\text{[}x^{2013}\left(x-1\right)+\text{1]}\)
\(=4\left(x^2+x+1\right)\text{[}\frac{x^{2013}\left(x-1\right)+1}{4}\text{]}\)
Rồi bạn làm các bước còn lại nhen :v
Lời giải của bạn Hà sai, lời giải của bạn Quang đúng.
Vì 5x4 chia hết cho 2x2;
–4x3 chia hết cho 2x2;
6x2y chia hết cho 2x2
Do đó A = 5x4 – 4x3 + 6x2y chia hết cho 2x2 hay A chia hết cho B.
Chú ý: Đơn thức A chia hết cho đơn thức B nếu tìm được đơn thức Q sao cho A=B.Q
Ví dụ : Cho hai đơn thức A= 2x2y3; B = 7xy
Khi đó với đơn thức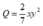
thì A=B.Q
Do đó, đơn thức A chia hết cho đơn thức B.