cho a,b>0; a+b=1. chứng minh \(\dfrac{1}{ab}+\dfrac{1}{a^2+b^2}\ge6\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
25 tháng 7 2017
a) We have :
a2 + b2 + c2 = ab + bc + ac
<=> 2a2 + 2b2 + 2c2 = 2ab + 2bc + 2ac
<=> 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ac = 0
<=> (a2 - 2ab + b2) + (b2 - 2bc + c2) + (c2 - 2ac + a2) = 0
<=> (a - b)2 + (b - c)2 + (c - a)2 = 0
\(\Leftrightarrow\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}}\Rightarrow a=b=c\)
25 tháng 7 2017
b) We have :
a2 - 2a + b2 + 4b + 4c2 - 4c + 6 = 0
(a2 - 2a + 1) + (b2 + 2.2b + 4) + (4c2 - 4c + 1) = 0
(a - 1)2 + (b + 2)2 + (2c - 1)2 = 0
\(\Leftrightarrow\hept{\begin{cases}a-1=0\\b+2=0\\2c-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=-2\\c=\frac{1}{2}\end{cases}}\)
R
18 tháng 2 2022
\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)
CM
28 tháng 5 2018
a) Chú ý m > 2 thì m > 0.
b) Chú ý a < 0 và b < 0 thì ab > 0. Khi đó a > b, nhân hai vế với 1 ab > 0 ta thu được 1 b > 1 a . Tương tự a > 0, b > 0, a > b ta được 1 a < 1 b .
TC
27 tháng 8 2017
tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha
15 tháng 2 2016
ôi dào !dễ ợt ! cô em mới cho học ngày hôm qua !k đi rùi em trình bày cho cách làm !
31 tháng 7 2021
a) a và b là 2 số tự nhiên ⇒ a, b ≥ 0
nếu a>0, b>0 ⇒a+b>0
nếu a>0, b=0 ⇒a+b>0
nếu a=0, b>0 ⇒a+b>0
nếu a=0, b=0 ⇒a+b=0
⇒ a+b=0 khi và chỉ khi a = b = 0
b) a và b là 2 số tự nhiên ⇒ a, b ≥ 0
nếu a>0, b>0 ⇒ ab>0
nếu a=0, b>0 ⇒ ab=0
nếu a>0, b=0 ⇒ ab=0
Vậy ab = 0 khi và chỉ khi a = 0 hoặc b = 0
16 tháng 9 2023
\(\sqrt[]{a+b}>\sqrt[]{a}-\sqrt[]{b}\) \(\left(a;b>0;a>b\right)\)
\(\Leftrightarrow\left(\sqrt[]{a+b}\right)^2>\left(\sqrt[]{a}-\sqrt[]{b}\right)^2\)
\(\Leftrightarrow a+b>a+b-2\sqrt[]{ab}\)
\(\Leftrightarrow2\sqrt[]{ab}>0\left(luôn.đúng\right)\)
Vậy \(\sqrt[]{a+b}>\sqrt[]{a}-\sqrt[]{b}\)
BL
2
21 tháng 7 2021
Ta có :
\(ac=b^2\Leftrightarrow\dfrac{a}{b}=\dfrac{b}{c}\left(1\right)\\ ab=c^2\Leftrightarrow\dfrac{b}{c}=\dfrac{c}{a}\left(2\right)\)
Từ (1) và (2) suy ra: \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}\)
Và \(a+b+c\ne0\)
Áp dụng tính chất dãy tỉ số bằng ta có :
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}=\dfrac{a+b+c}{b+c+a}=1\\ \Rightarrow a=b=c\)
Ta có :
\(\dfrac{b^{3333}}{a^{1111}.c^{2222}}=\dfrac{b^{3333}}{b^{1111}.b^{2222}}=\dfrac{b^{3333}}{b^{3333}}=1\)
Vậy \(\dfrac{b^{3333}}{a^{1111}.c^{2222}}=1\)
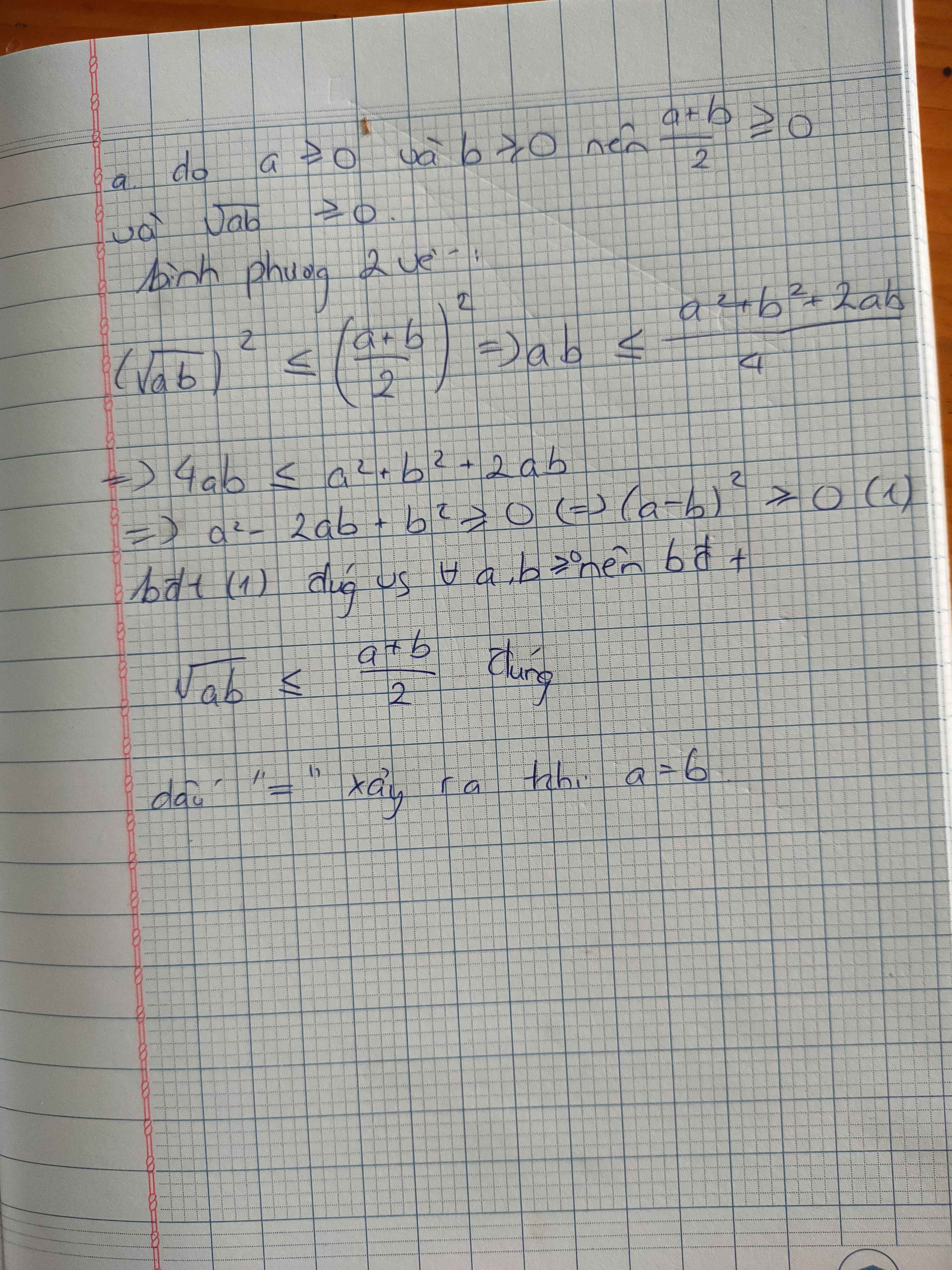
Đặt \(C=\dfrac{1}{ab}+\dfrac{1}{a^2+b^2}\)
\(C=\dfrac{1}{2ab}+\dfrac{1}{2ab}+\dfrac{1}{a^2+b^2}\)
Ta có:\(2ab\le\dfrac{\left(a+b\right)^2}{2}\)(tự cm)
\(\Rightarrow\dfrac{1}{2ab}\ge\dfrac{1}{\dfrac{1}{2}}=2\)
Lại có:\(\dfrac{1}{2ab}+\dfrac{1}{a^2+b^2}\ge\dfrac{4}{a^2+2ab+b^2}=\dfrac{4}{\left(a+b\right)^2}=4\)(tự cm)
\(\Rightarrow C\ge2+4=6\left(đpcm\right)\)